Le tournesol
Les graines de tournesol forment des spirales sur la fleur. 55 et 89 très précisément. Ce sont des nombres de la suite de Fibonacci.
1
1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8 + 13 = 21
13 + 21 = 34
21 + 34 = 55
34 + 55 = 89En retirant les graines de tournesol une à une, on arrive bien à compter les spirales.
Lors de sa croissance chaque graine est positionnée avec un angle constant par rapport à la précédente.
% Angle = 137,5
Si on prend n’importe quelle autre mesure d’angle, on va avoir de la place perdue:
% Angle = 130
Si 
est un nombre rationnel, les graines se retouveront alignées ce qui n’est pas optimal car les feuilles se feront de l’ombre, de la place sera perdu etc. Quel est le nombre irrationnel le plus éloigné des nombres rationnels 
de taille finie (c’est-à-dire avec p et q petits) ?
Le nombre d’or, souvent noté 
, est défini comme
![\[ \phi = \frac{1 + \sqrt{5}}{2}. \]](https://eva.louis-le-grand.net/maths/wp-content/ql-cache/quicklatex.com-d9d39026125e332a4d6e0b837a7a1be3_l3.png "Rendered by QuickLaTeX.com")
est solution de l’équation : 
![\[ \phi = 1 + \frac{1}{1 + \frac{1}{\phi}}. \]](https://eva.louis-le-grand.net/maths/wp-content/ql-cache/quicklatex.com-082227d46e0b5980552337592c0a2ab6_l3.png "Rendered by QuickLaTeX.com")
ou encore
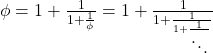
Sous la forme suivante, on comprend bien que les entiers 
doivent être aussi petits que possible pour que l’erreur d’approximation soit la plus grande et donc que notre nombre soit aussi loin que possible des rationnels.
Ce qui arrive pour 
, 
, 
… et on tombe donc sur le nombre d’or.
Que ce soit les tournesols, les chou-fleurs, des Choux Romanesco, de sont toutes des fleurs qui sont restées collées et qui ne se sont pas écartées lors de la croissance des tiges. Il en est de même avec les artichauts qui savent compter jusqu’à ?
Pour l’anecdote, si vous n’avez pas de pince à épiler et que voulez juste récupérer les graines de tournesol vite fait, voici la méthode:
Source: TikTok naturesms
Les artichauts
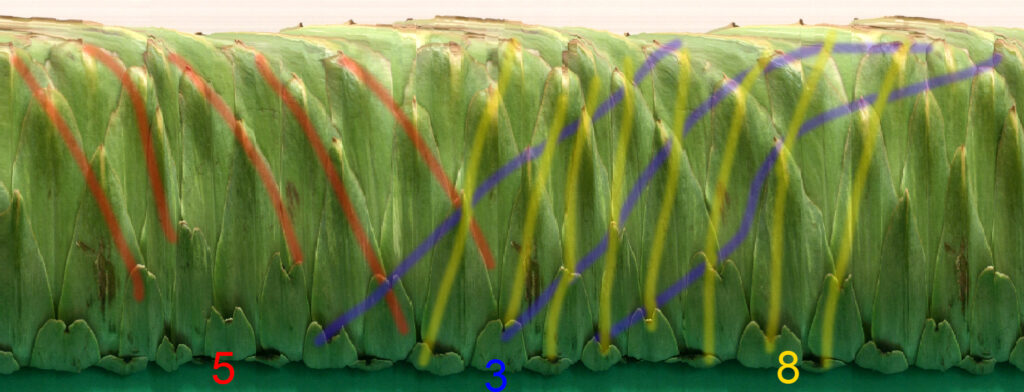
55 spirales bleues
et 89 spirales rouges.
La figue de barbarie
L’ananas
pareil !
Sauf les mauvaises copies d’ananas comme ce verre à cocktail qui a pourtant du succès. Vous voyez le problème ? Il est symétrique alors que tous les ananas sont gauches.
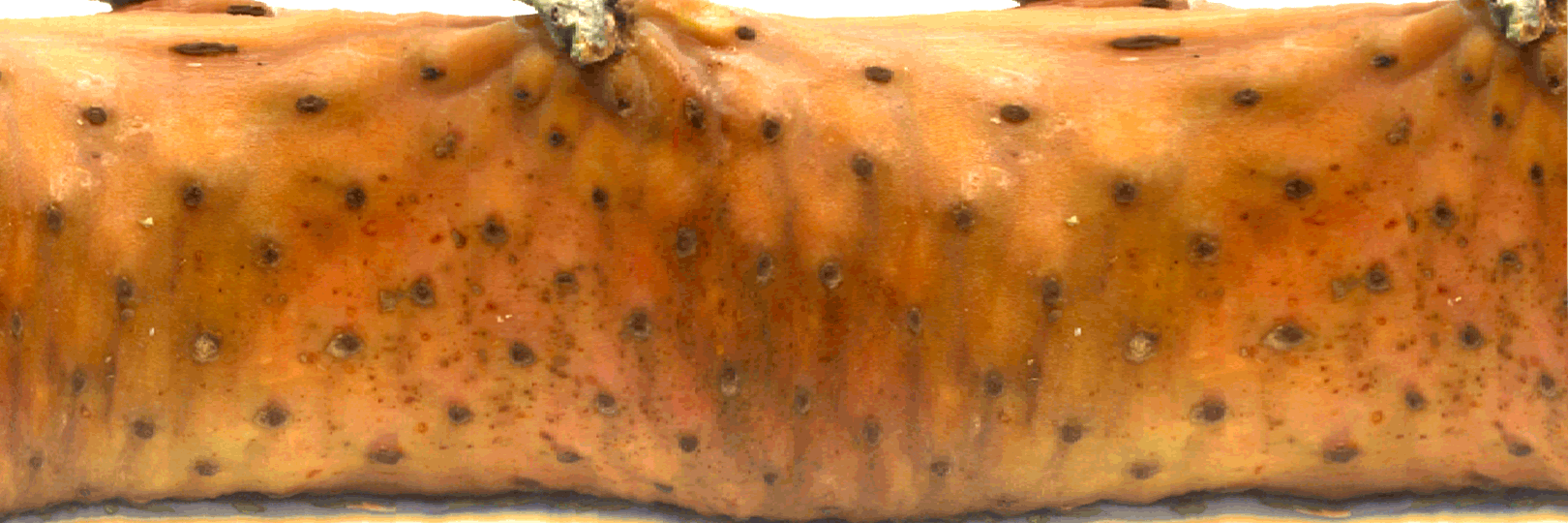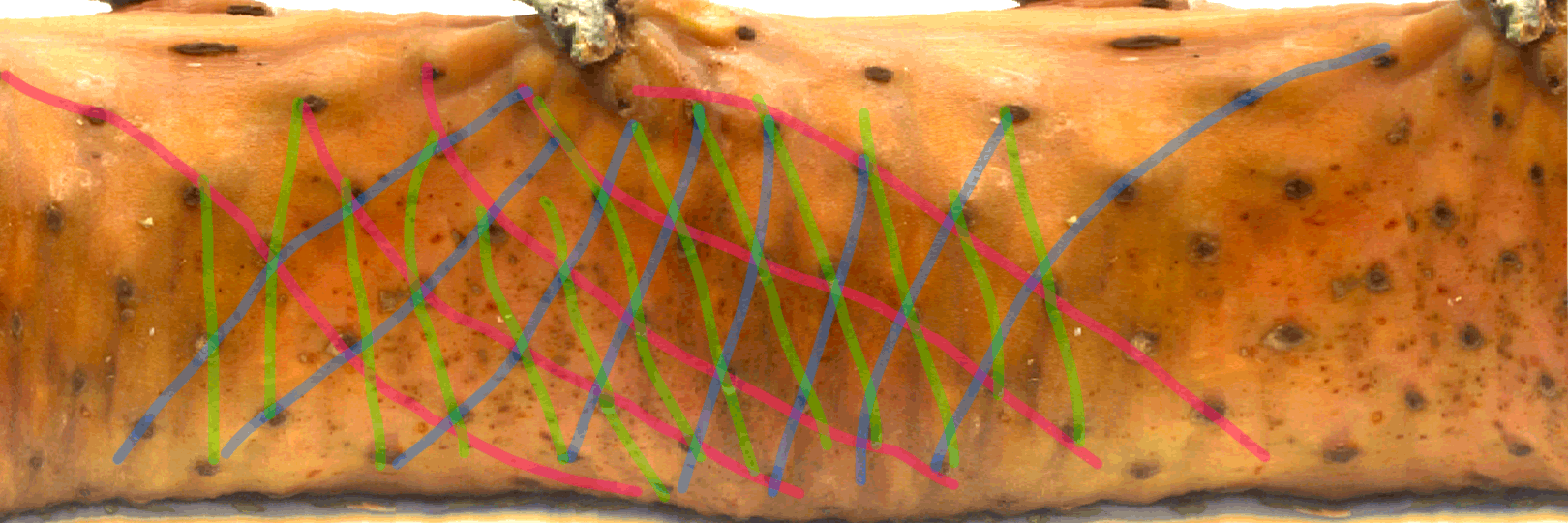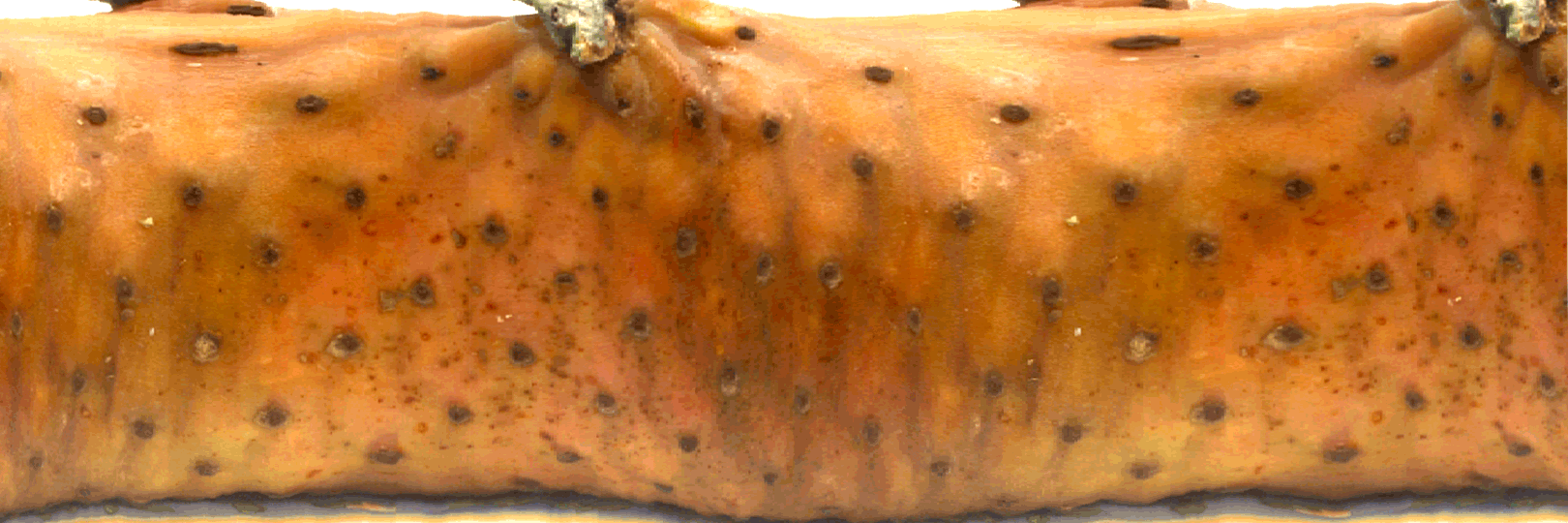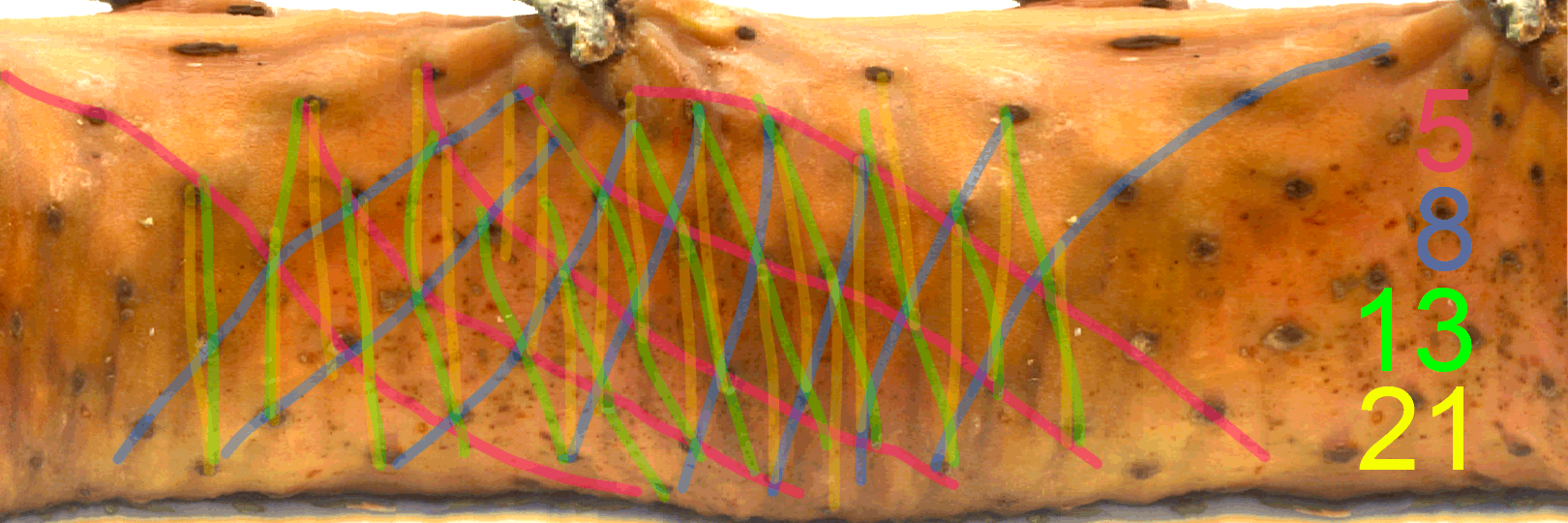
L’ananas a en vrai 5 spirales dans un sens et et 8 spirales dans l’autre; ou 13 mais toujours des nombres successifs de Fibonacci.
On a du mal à voir sans faire le tour, donc voici une photo de l’ananas virtuellement aplati.
Voici les spirales:
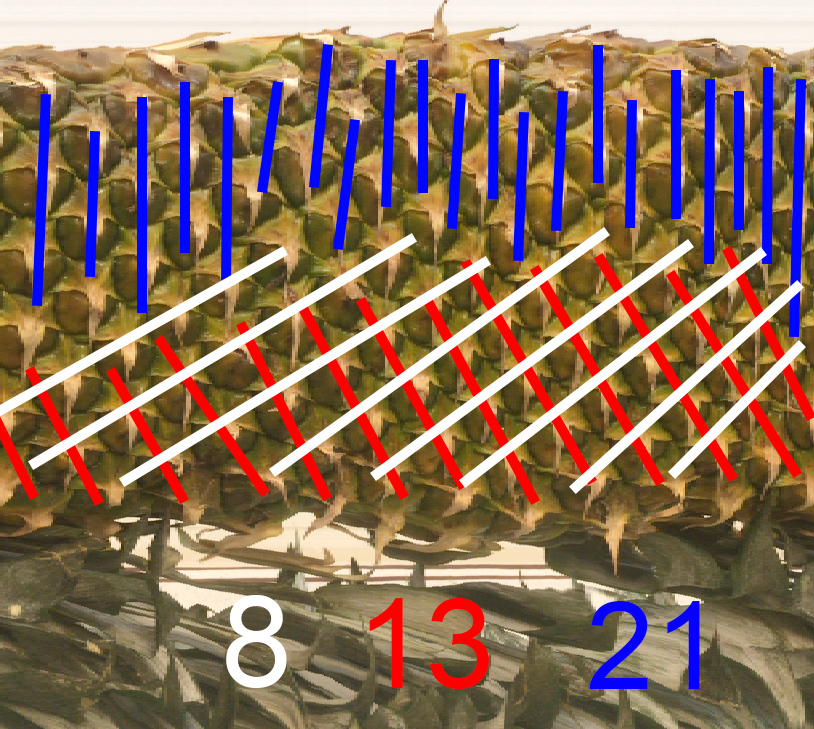
Lien vers l’appli web maison pour prendre une telle photo avec votre iphone en faisant tourner l’ananas devant l’objectif.
Voici un autre ananas:
Cette Nature morte à l’ananas de Henri Manguin de 1929 exposée au Musée Beaubourg est donc un faux.
Voici 3 courbes. lesquelles peuvent représenter un Ananas ?
A:
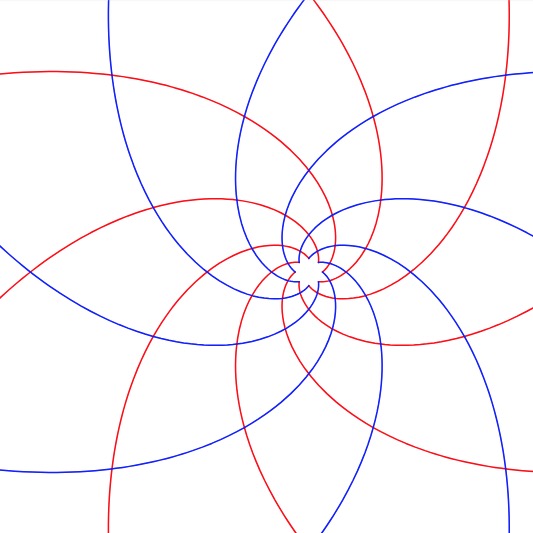
B:
C:
Chou rouge
pareil ?
InspirationPour aller plus loin et comprendre le cas du maïs avec Stéphane Douady:
