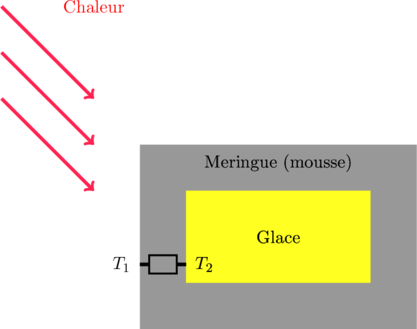
L’omelette norvégienne a été inventée suite à la modélisation de la chaleur et aux mesures d’isolation du blanc d’oeuf en neige, pour faire un gâteau moderne issu de la science et de la technologie.
Un glace entourée de meringue italienne est enfournée pour cuire et faire colorer la meringue. Pourtant la glace à l’intérieur reste glacée.
Sur l’analogie mathématique Chaleur-Electricité … mais qui a ses limites en physique
On connait bien U=RI en électricité, mais on connait moins souvent l’équation de la chaleur qui l’a historiquement précédé dont on faite le bicentenaire en 2023. Ohm a remarqué l’analogie en 1827 avec entre les prémices de l’électricité et la théorie de la chaleur, et croyant seul à cette analogie (contrairement à Laplace par exemple) cela le conduisit à établir la loi d’Ohm.
Dans sa théorie analytique de la chaleur, Fourier avait établi les séries infinies de Fourier et vérifié leur convergence. Mais Ohm physicien et non mathématicien a repris l’analogie des séries de Fourier mais en les traitant juste comme des polynômes finis.
Maxwell écrit en 1873 Electricité et Magnétisme:
En électrostatique, il existe entre le potentiel et l’électricité le même rapport qu’il y a en Hydrostatique entre la pression et le fluide, et en Ther- modynamique entre la température et la chaleur. L’électricité, le fluide, la chaleur tendent à passer d’un endroit à un autre, si le potentiel, la pression, la température sont plus élevés au premier point qu’au second. Un fluide est certainement une substance, et certainement aussi, la chaleur n’est pas une substance : donc, si nous pouvons tirer profit d’analogies de ce genre, pour nous faire une idée nette des relations qui existent entre les quanti- tés électriques, nous devons bien prendre garde que l’une ou l’autre de ces analogies ne nous induise à croire que l’électricité est une substance comme l’eau, ou un état de mouvement comme la chaleur. […]
L’analogie entre la théorie de la conduction de l’électricité et la théorie de la conduction de la chaleur est, à première vue, presque complète (*). Si nous prenons deux systèmes géométriquement semblables, et tels que la conductibilité calorifique d’une partie du premier soit proportionnelle à la conductibilité électrique de la partie correspondante du second, et si l’on fait la température de chaque partie du premier proportionnelle au potentiel électrique de la même partie du second, le flux de chaleur à travers une aire quelconque prise dans le premier sera proportionnel au flux d’électricité à Évolution des analogies. L’exemple de l’analogie chaleur–électricité travers l’aire correspondante dans le second
Electricité
∆U: différentiel de potentiels U électrique
I: Intensité (Flux de charges électriques à un instant donné
R: Résistance électrique
c: conductibilité électrique
Loi d’Ohm: ![]()
![]()
où L est l’épaisseur du matériau, S sa surface et ![]() la résistivité.
la résistivité.
Chaleur
∆T: différence de températures T
![]() : Flux de chaleur, ou flux thermique à un instant donné
: Flux de chaleur, ou flux thermique à un instant donné
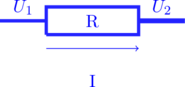
R: résistance thermique
c: conductibilité calorifique
Loi de Fourier: ![]()
![]()
où L est l’épaisseur du matériau, S sa surface et ![]() la conductivité thermique.
la conductivité thermique.

Les résistances se combinent en série ou en parallèle de la même façon.
En Série on a :
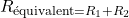

En parallèle on a:
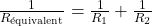

Mais l’analogie a ses imites:
(*) Maxwell ajoute:
La différence entre les phénomènes consiste dans ce fait : que les corps sont susceptibles d’absorber la chaleur et de l’émettre, tandis qu’ils n’ont point la propriété correspondante pour l’électricité.
On ne peut échauffer un corps sans lui fournir une certaine quantité de chaleur dépendant de sa masse et de sa chaleur spécifique; le potentiel électrique, au contraire, peut être élevé à un degré quelconque, de la façon que nous avons déjà décrite, sans communiquer au corps aucune charge d’électricité.
Supposons encore un corps préalablement chauffé et placé à l’intérieur d’un vase clos. L’extérieur du vase sera d’abord à la température des objets environnants, s’échauffera bientôt et restera chaud tant que la chaleur du corps intérieur n’aura pas fini de s’échapper.
Il est impossible de faire l’expérience électrique correspondante. Il est im- possible d’électriser un corps et de le placer dans un vase creux, de façon que l’extérieur du vase ne montre d’abord aucune trace d’électrisation et devienne ensuite électrisé. Ce sont des phénomènes de ce genre que Faraday a recherchés en vain sous le nom de charge absolue d’électricité.
La chaleur peut être cachée à l’intérieur d’un corps et n’avoir point d’action au dehors : mais il est impossible d’isoler une quantité d’électricité, de l’empêcher d’être constamment reliée par induction à une quantité d’électricité contraire.
Il n’y a donc rien dans les phénomènes électriques qui corresponde à la capacité calorifique. C’est ce qui résulte immédiatement de l’hypothèse suivie dans cet ouvrage, que l’électricité est soumise à la même condition de continuité que les fluides incompressibles. Il est donc impossible de donner à un corps une charge effective d’électricité, en forçant une quantité
Heaviside écrit aussi que l’analogie mathématique a en effet permis à la théorie de l’électricité de progresser, mais ensuite les théories ont suffisamment muri pour diverger:
- – les deux théories ne sont pas strictement comparables. L’analogie négative reprend le pas car il existe des différences importantes comme l’auto-induction (câbles téléphoniques), l’isolation électrique est possible alors que l’isolation thermique ne l’est pas. . .
- – les deux théories peuvent être autonomes et consacrées à la résolution de problèmes spécifiques. Quand la théorie a suffisamment progressé, elle prend ses distances, son indépendance par rapport à la théorie mère dans l’analogie. On doit les utiliser, à l’intérieur de leur domaine de validité respectif, à la résolution de problèmes spécifiques.
Feynman:
On peut aussi résoudre les problèmes aux limites par des mesures sur des analogues physiques. L’équation de Laplace se présente dans de nombreux cas physiques différents : dans la propagation de la chaleur en régime permanent, dans l’écoulement irrotationnel d’un fluide, dans l’écoulement d’un fluide dans un milieu étendu, et dans la déformation d’une membrane élastique. Il est fréquemment possible de réaliser un modèle physique qui est analogue au problème électrique que nous voulons résoudre. On peut dé- terminer la solution du problème auquel on s’intéresse en mesurant une quantité analogue convenable sur le modèle.
– Voici un exemple d’analogie électrique amusante avec des chaines et des rotations.
Omelette Norvégienne

Attention aux glaces du commerce, elles sont dénaturées pour fondre rapidement et rester molle en pouvant être consommées dès que sortie du congélateur (contenant air et sirop de glucose). Prendre plutôt une bonne vieille glace à la vanille traditionnelle.
La meringue italienne est constituée d’oeuf battu auquel on ajoute du sucre bouilli (5 blancs pour 200g de sucre). Le résultat est une mousse avec des bulles d’air emprisonnées dans de l’eau et protéines et sucre. Les bulles ont pour diamètre de 0.01mm à 0.1mm e ne sont pas toutes rondes:

Mais à quelle température est-il mieux de manger une glace ?
On apprend dans le livre « Mes
copains, les maths et moi » de Edward van de Vendel que:
« nos glaces sont servies à une température de 12 degrés au dessous de zéro, mais que la glace américaine est sera servie à 11 degrés… au dessus de zéro. »
et que les italiens les servent à 5 degrés au dessous de zéro car elles leur glaces contiennent moins de gras et moins d’air.
On l’aura compris, les américains utilisent les degrés Fahrenheit.

Bibliographie :
Sur analogie Chaleur-Electricité: Évolution des analogies – L’exemple de l’analogie chaleur–électricité, Etienne Bolmont LPHS