6 cookies carrés à partager en 42.

Voici un cookie carré décoré

On veut le partager en 7. Voici un partage possible.
1) 7 bandes

Mais comment découper 1/7ème ?
2) à partir de découpes en 2 et aux nombres binaires:
Un algorithme de découpe de gâteau
1/7ème s’écrit en décimal: 1/7 = 0,142857 142857 142857…10 et en binaire: 1/7 = 0,001 001 001 001 …2.
En effet, il n’y a qu’à poser la division de 1 par 7 en binaire:
1 | 111
+---------
| 0
|
1 | 111
10 +---------
| 0,0
|
1 | 111
10 +---------
100 | 0,00
|
1 | 111
10 +---------
100 | 0,001 0...
1000 |
- 111 |
= 1 |
10D’où l’algorithme pour donner à la première personne 1/ème du gateau:
On coupe en 2 ce qu'on a à découper.
On garde un des 2 morceaux.
On coupe en 2 le reste.
On garde un des 2 morceaux.
On donne l'autre à la première personne.
On regroupe tous les morceaux qu' on a gardé, et avec on recommence tant qu'il reste quelque chose de pas trop petit à découper.







Mais cette technique fait beaucoup de miettes de cookie. Ne pourrait-on pas utiliser le fait que les cookies sont carrés ?
3) repérer 1/7e de la longueur du coté d’un carré ?
Construction pour SEPT bandes
Plus grande puissance de 2 inférieure à 7 : 4
Fraction: (7 – 4) / 4 = 3 / 4
Milieu de BC, puis milieu de CE: point F.
Le point F est au trois-quarts de BC.
Tracer AF et BD: point G.
Parallèle à BC en G.
Le point G se trouve à la fraction (7 – 4) / 7 = 3/7 de HI. Alors: HG = 3/7 HI et GI = 4/7 HI.
Milieu J de GI, puis milieux de IJ et de JG.
Report de IK sur GH (ouverture d’un compas) en GM, MN et NH.
Le segment IH est divisé en sept.
Tracer les six parallèles à AB pour obtenir les sept bandes.


4) Mais certains auront tout le bord !
D’autres que le milieu, ce n’est pas juste.
Voici un autre partage possible. On fait 7 parts de 51,4°
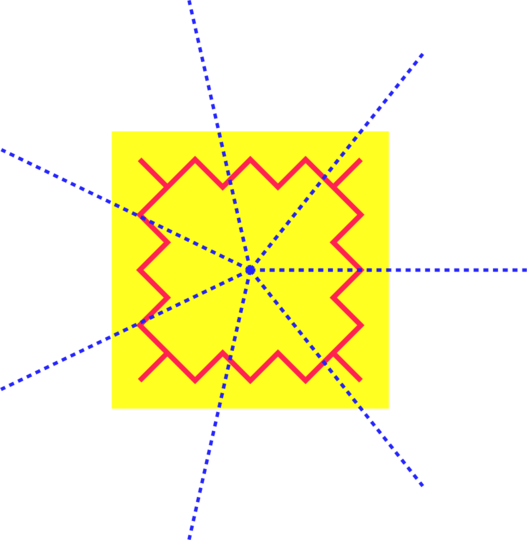
Les parts ont toutes du bord à peu près également, mais il y a des parts plus grandes, celles dans les coins.
5) 7 parts de même aire, avec autant de bord:
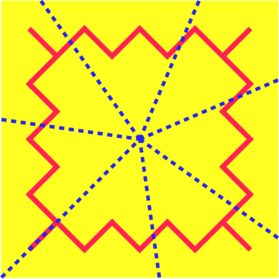
Pourquoi ça marche ?
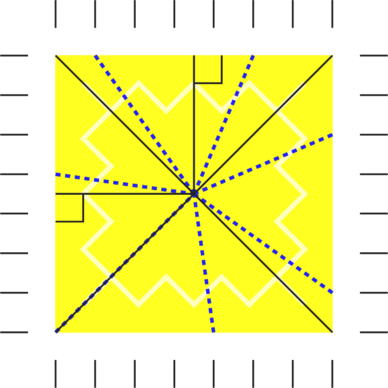
L’aire d’un triangle est ![]() Chaque part est un triangle ou la somme de 2 triangles qui ont tous les même longueur de hauteur, et la même longueur de base.
Chaque part est un triangle ou la somme de 2 triangles qui ont tous les même longueur de hauteur, et la même longueur de base.
6) Mais peut être que seuls certains préfèrent le bord
On va utiliser la méthode du couteau qui bouge.
On commence avec le couteau au bord et on le déplace progressivement de part en part. Dès qu'une des 7 personne est satisfait de la part en train d'être découpée, il dit stop, on tranche et il récupère sa part.
On recommence ensuite avec les 6 autres personnes qui restent et le reste de gateau.
Et ainsi de suite.
Par exemple, si tous préfèrent le bord sauf une personne, on pourrait obtenir le découpage suivant qui est meilleur pour tous que les précédentes méthodes.
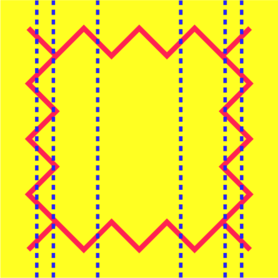
Mais il peut y avoir des jaloux. Ou même des personnes qui souhaiteraient au final s’échanger des parts. Mais ça, c’st une autre histoire, on a plus de cookie à partager.

