Soit la transformation du plan complexe 
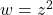
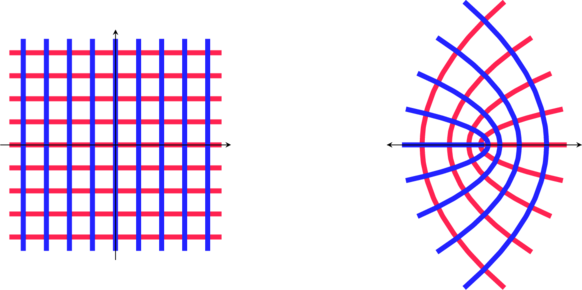
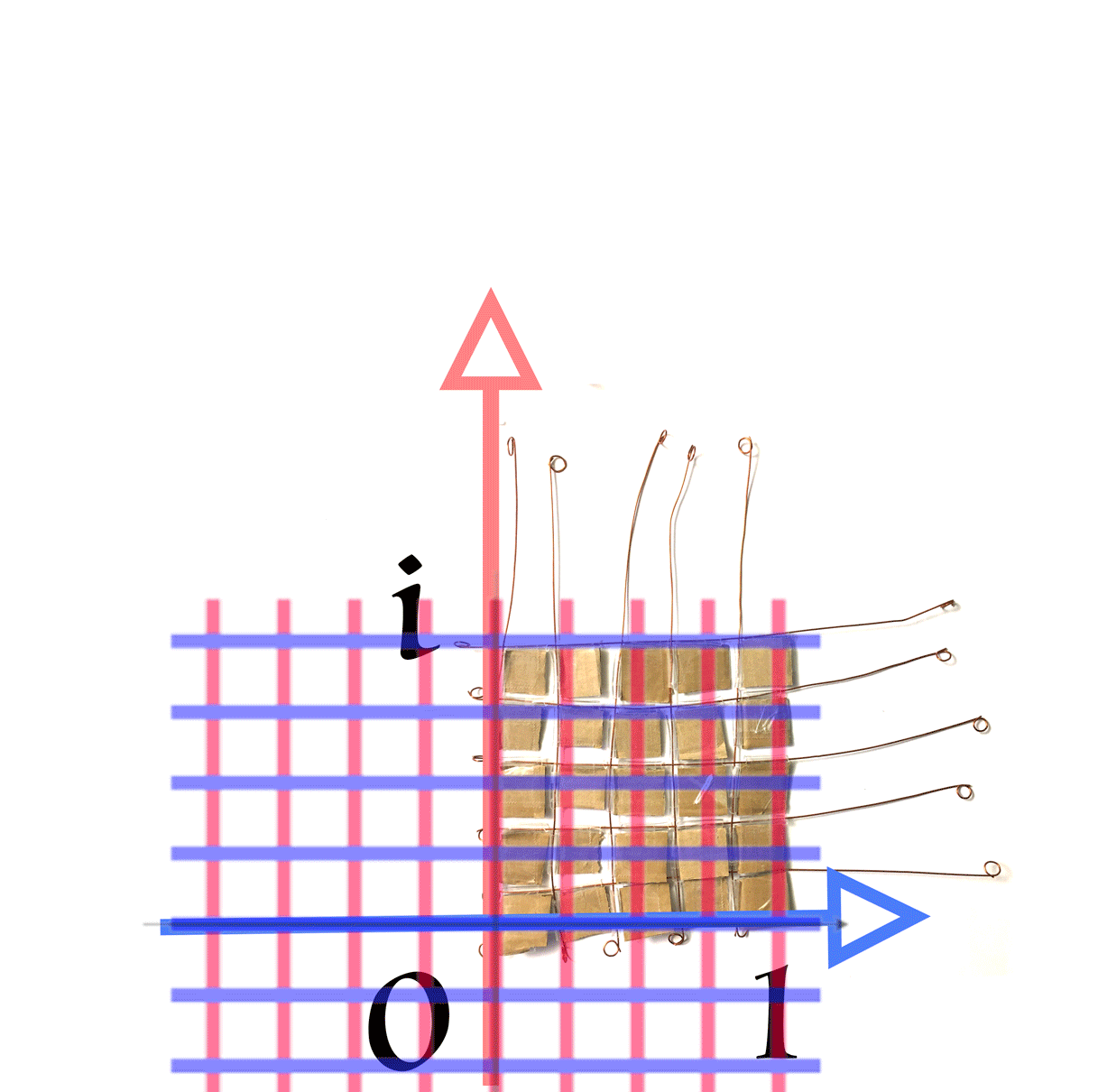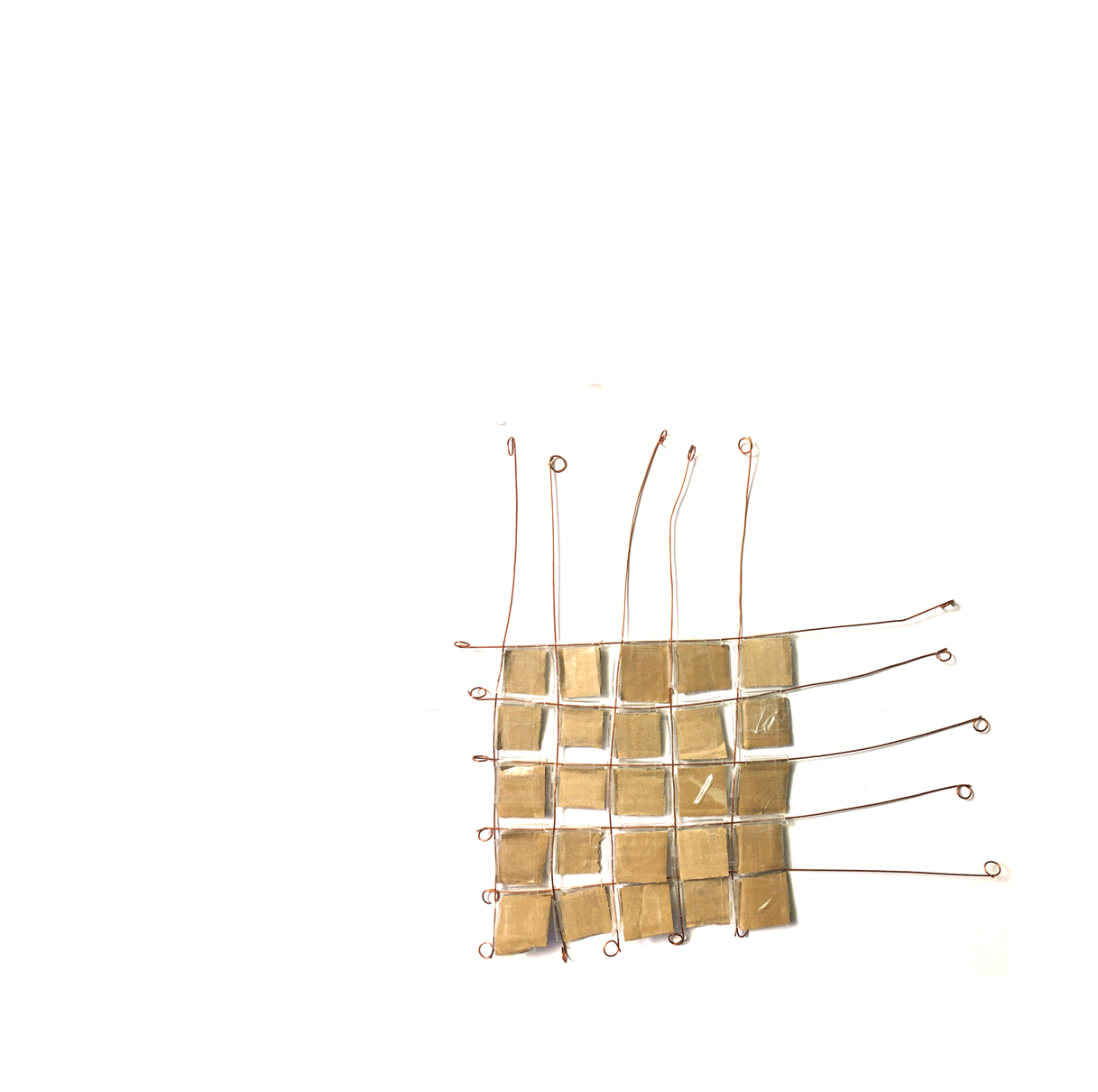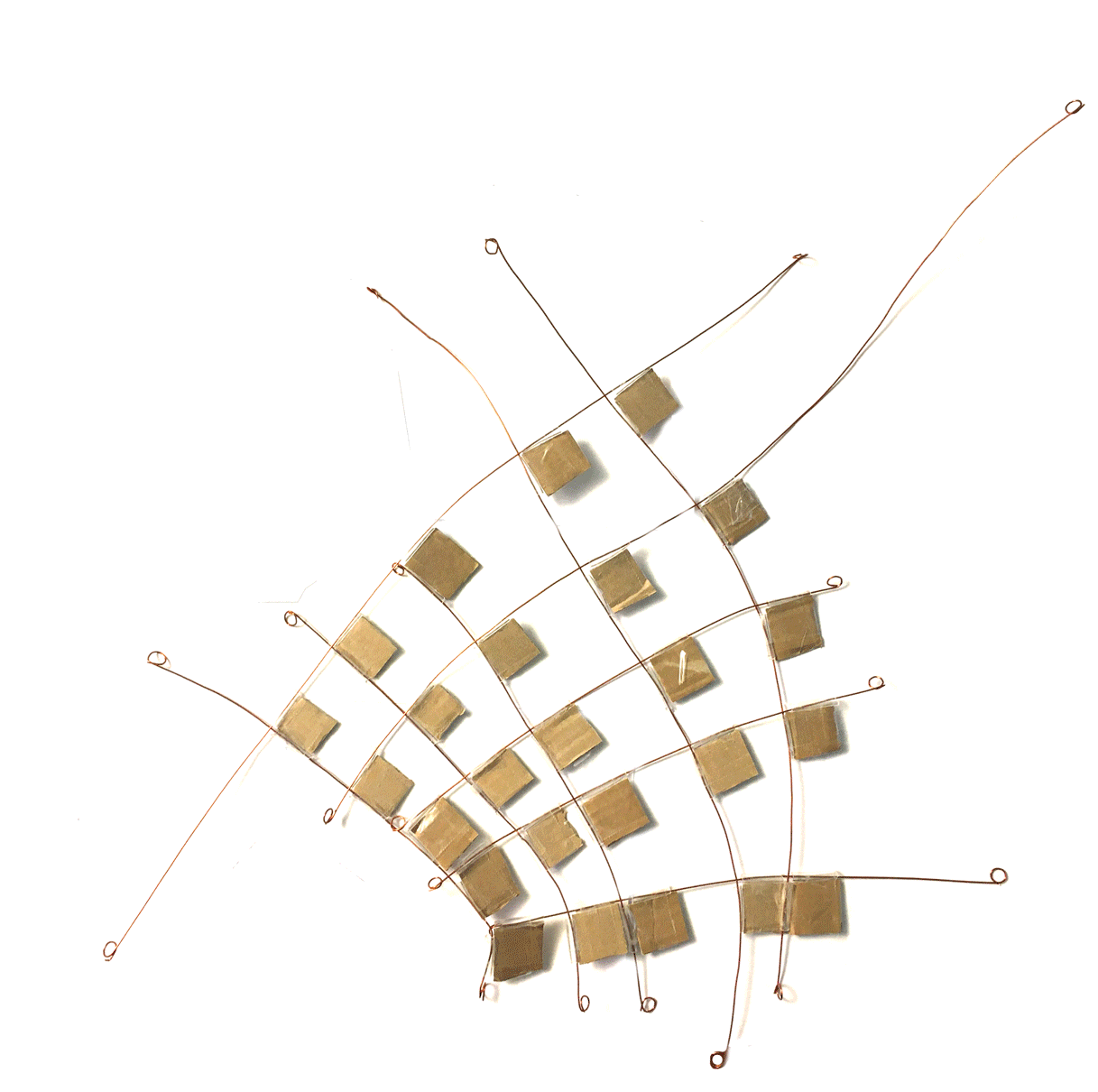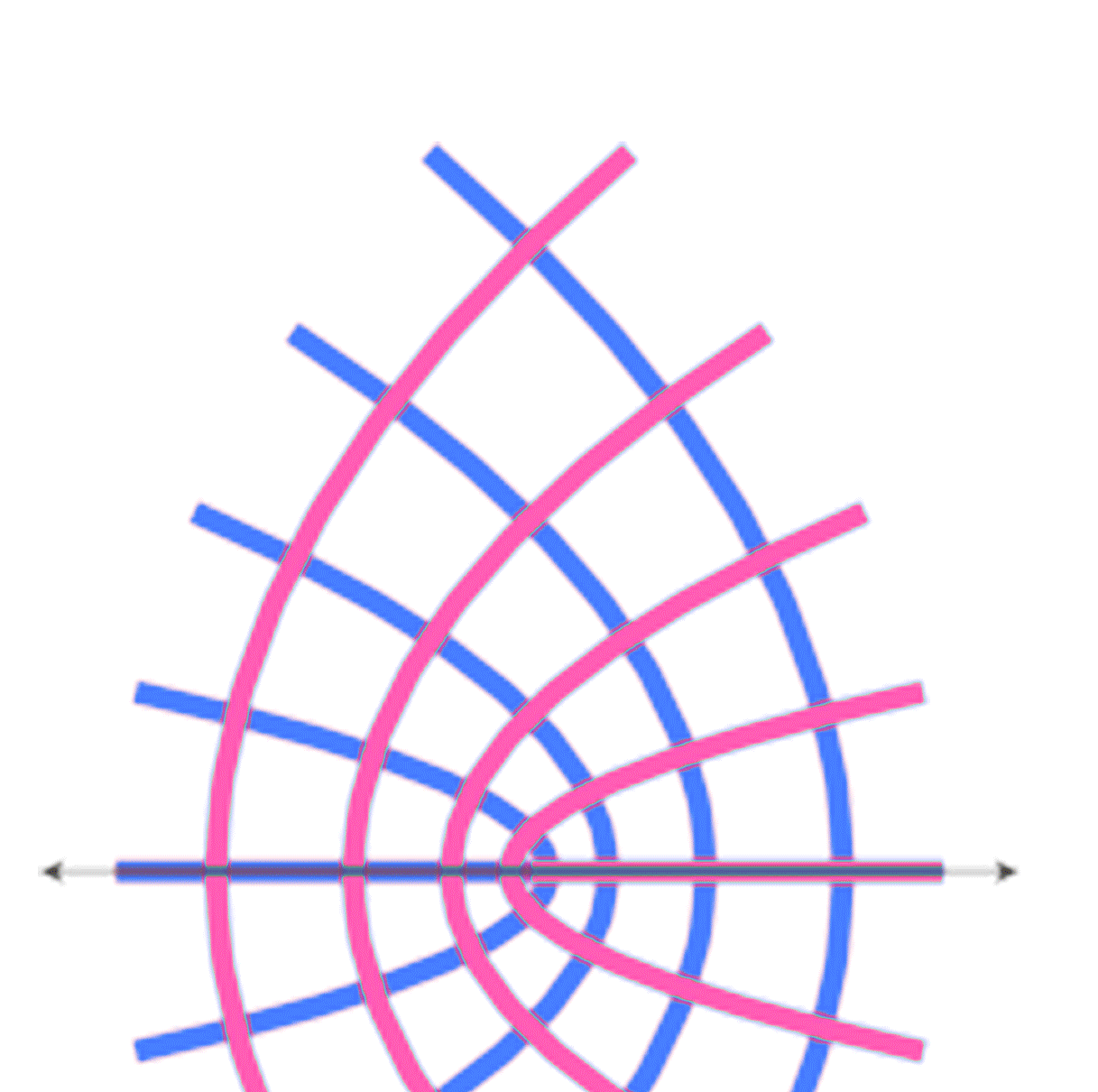
Voici la Flamenkuch équivalente:
A présent, voici d’autres transformations, à associer aux autres Flamenkuch:
, ., 
, 
, 
, 
…
Voici les réponses:
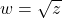
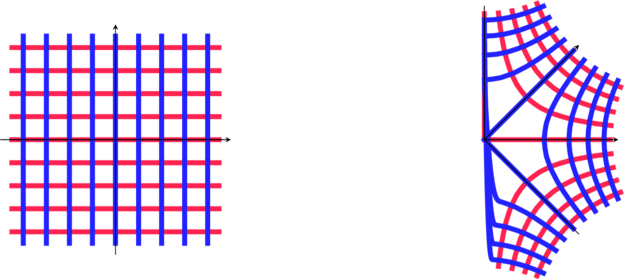
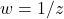
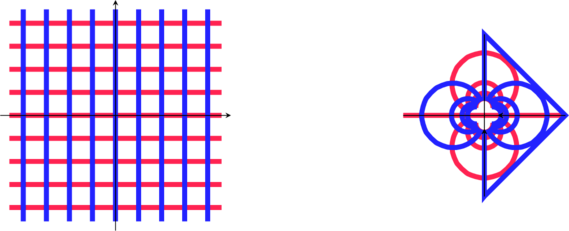
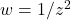
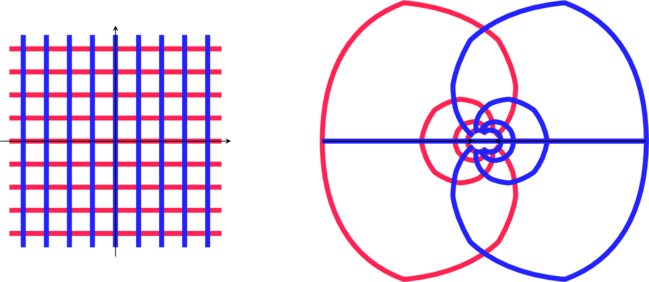
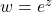
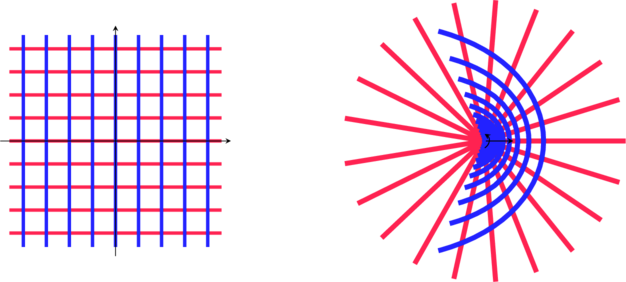
Enfin voici d’autres transformations:
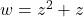
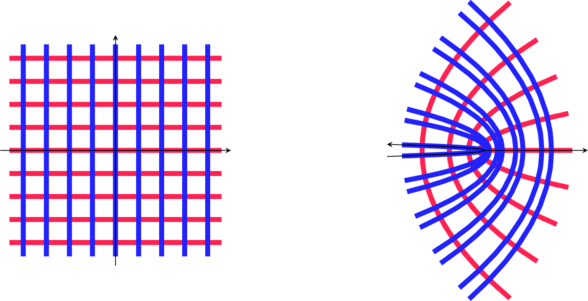
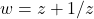
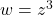
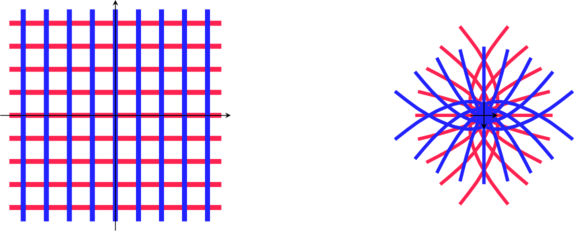
et
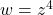
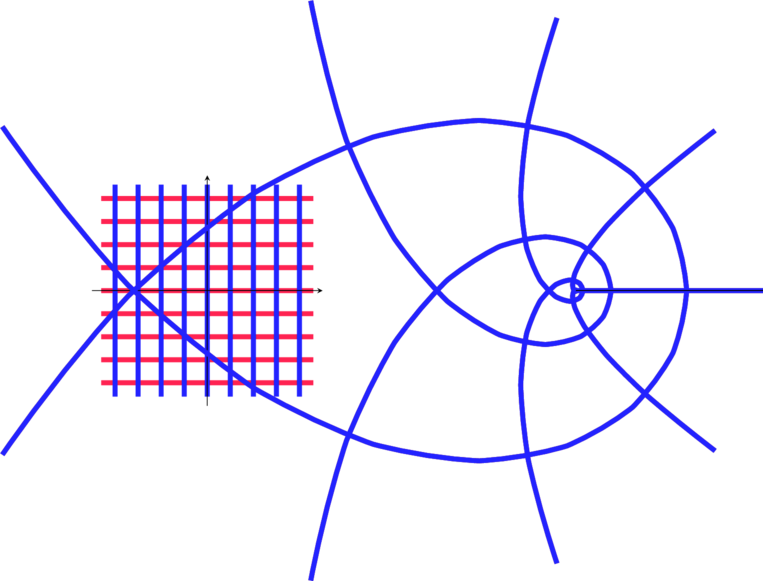
Mot clé en anglais: « Conformal map« : comforme signifie ici qui conserve les angles. ce qui est le cas pour ces transformations sauf en quelques points particuliers.
Cette conservation d’angle est importante pour les application en cartographie, car on aime bien conserver les cap (30°Nord parexemple) quand on suit une trajectoire.
Comme les angles droits sont conservés, on a aussi des applications pour représenter des champs de potentiels et courbes équipotentielles.
Pour aller plus loin