Gâteau de Villarceau

Par 1 point du tore, il passe 4 cercles.

Comme l’illustrent ces gratins de spaghettis toriques, par un point du tore, il passe 2 cercles, un ‘horizontal’ en rose et un ‘vertical’ en bleu, et deux cercles de Villarceau en vert et son symétrique.

On peut aussi obtenir une courbe en forme de 8

Asymptote:

Autre exemple:

Avec Asymptote:

\begin{asy}

settings.render = 8;
settings.prc = false;

import graph3;
import contour;
size3(8cm);

currentprojection = orthographic(10,1,4);
defaultrender = render(merge = true);

// create torus as surface of rotation
int umax = 40;
int vmax = 40;
surface torus = surface(Circle(c=2Y, r=0.6, normal=X, n=vmax), c=O, axis=Z, n=umax);
torus.ucyclic(true);
torus.vcyclic(true);

pen meshpen = 0.3pt + gray;

draw(torus, surfacepen=material(diffusepen=white+opacity(0.6), emissivepen=white));
for (int u = 0; u < umax; ++u)
  draw(torus.uequals(u), p=meshpen);
for (int v = 0; v < vmax; ++v)
  draw(graph(new triple(real u) {return torus.point(u,v); }, 0, umax, operator ..),
       p=meshpen);

pair a = (floor(umax/2) + 2, 3);
dot(torus.point(a.x, a.y), L="", align=W);
pair b = (5, floor(vmax/2));
dot(torus.point(b.x, b.y), L="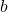", align=2Z + X);

path3 abpath(int ucycles, int vcycles) {
  pair bshift = (ucycles*umax, vcycles*vmax);
  triple f(real t) {
    pair uv = (1-t)*a + t*(b+bshift);
    return torus.point(uv.x, uv.y);
  }
  return graph(f, 0, 1, operator ..);
}

real linewidth = 0.8pt;

draw(abpath(0,0), p=linewidth + orange);
draw(abpath(1,0), p=linewidth + red);
draw(abpath(1,-1), p=linewidth + darkgreen);
\end{asy}