Voici un triangle rempli de billes. SI je le déforme avec une aire constante, les billes resteront juste à l’intérieur.
En gardant la base immobile et constante, je peux déplacer le sommet opposé suivant une parallèle à la base. Je suis ainsi assuré de pouvoir déformer le triangle avec un aire constante.






Pour bien comprendre comment la surface est déformée, je peux remplacer les billes par des bandes qui peuvent glisser les unes sur les autres.
On réalise ainsi que chaque hauteur de couche reste à sa hauteur au cours de la déformation.
On comprend alors bien pourquoi le théorème du théorème glissé est juste.
On peut appliquer cela pour déformer un triangle en un triangle rectangle. Ce triangle est alors la moitié d’un rectangle. D’où l’aire du triangle qui est la moitié de l’aire du rectangle. Comme l’aire du rectangle est largeur x hauteur, autrement dit ici base x hauteur, en le divisant par deux, on obtient bien la formule base x hauteur divisé par deux.
Volume d’une pyramide
On peut appliquer le même principe pour un volume et une pyramide en particulier.
Si on prend une forme quelconque coupé en tranche, on peut déplacer les tranches, sans en changer le voulme.
Les deux volumes suivant ont évidement le même volume.


Coupons un cube en 3 parties ainsi. Ce sont trois parties égales donc ayant pour volume celui du cube divisé par trois.
Prenons une pyramide, et on peut déplacer les couches pour former n’importe quelle pyramide à base carré avec pour hauteur le coté du cube. Toutes ces pyramides ont donc pour volume 1/3 du volume du cube. Base x Hauteur divisé par trois.
Volume Pyramide: 1/3 Base x Hauteur
Si on allonge une pyramide dans une direction d’un facteur f, le volume sera agrandi du même facteur f. On réalise ainsi que le volume d’une pyramide quelconque a bien pour formule de volume :
Volume Pyramide: 1/3 Base x Hauteur
Et on peut généraliser facilement aux pyramides à base triangulaire, (moitié du carré de base). ET à toute surface de base (que l’on peut découper en petits triangles), y compris le volume d’un cône, qu’il soit droit ou penché.
Aire d’une cyloïde
Au début du siècle xx, on problème qui occupait beaucoup était de connaitre l’aire sous la courbe d’une cycloide.
Intégrale
On découpe en petites tranches que l’on ajoute.
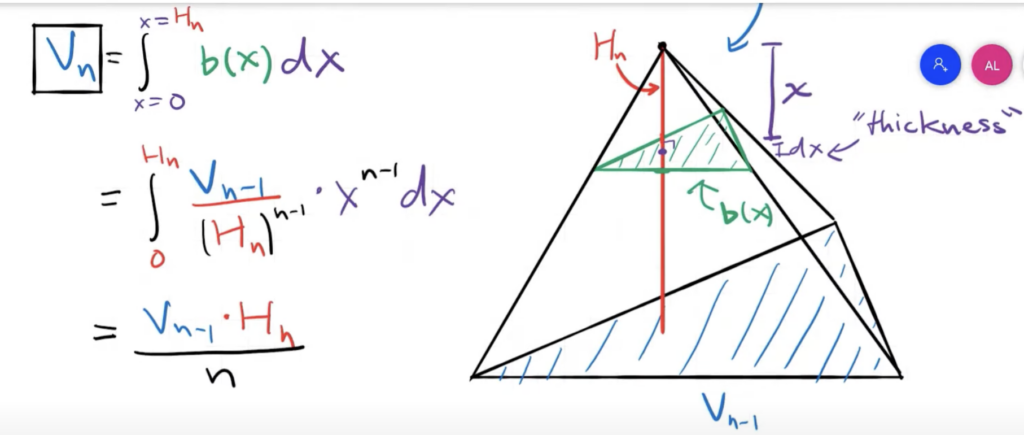
Volume d’une pyramide en dimensions 4
Base (du tetrahedre) x Hauteur / 4
Base (du triangle) x Hauteur / (3*4)
Base (=coté) x Hauteur / (2*3*4)?
…
Hypervolume: https://fr.wikipedia.org/wiki/4-polytope_r%C3%A9gulier_convexe
https://www.apmep.fr/IMG/pdf/AAA05020.pdf
https://hal.science/tel-02459860v1/file/Skapin_These_2001.pdf
https://community.wolfram.com/groups/-/m/t/1150337