Partage de pizza

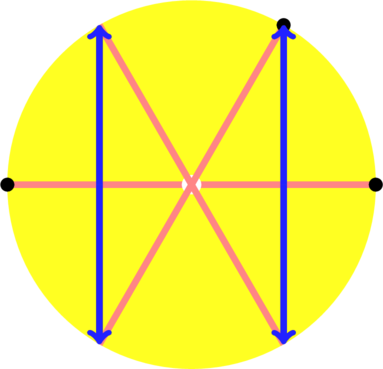
Larry Carter & Stan Wagon (1994) Proof without Words: Fair Allocation of a Pizza, Mathematics Magazine, 67:4, 267-267, DOI: 10.1080/0025570X.1994.11996228

Théorème du sandwich au jambon

Inspiration
Podcastscience:
Plutôt que de tenter une démonstration générale bien trop compliquée, je vais tenter de vous donner une idée de démonstration pour le sandwich SNCF, autrement dit le sandwich de dimension 2, avec deux ingrédients : du pain, et du jambon.
Prenez une direction de coupe, n’importe laquelle. Il existe nécessairement un endroit où on peut couper le pain en deux parties égales en suivant cette direction; il suffit pour s’en convaincre de faire passer le couteau au-dessus du pain en le gardant toujours dans la même direction. Une fois qu’on a repéré cet endroit, de deux choses l’une : soit le jambon est également coupé en deux parts égales, et on est content, soit ce n’est pas le cas. Alors il y a plus de jambon d’un côté du couteau que de l’autre. L’idée est de dire que si on tourne progressivement le couteau, en le déplaçant en même temps toujours à l’endroit où le pain est coupé en deux parties égales, la différence entre les quantités des deux morceaux de jambon obtenus à chaque fois va varier de façon continue. Or une fois que l’on a effectué un tour complet, cette différence est exactement l’opposée de celle observée au début. On est donc passé de plus de jambon d’un côté de la lame à plus de jambon de l’autre côté de la lame. Le théorème des valeurs intermédiaires et le bon sens nous disent donc qu’à un moment donné, il y avait autant de jambon des deux côtés…

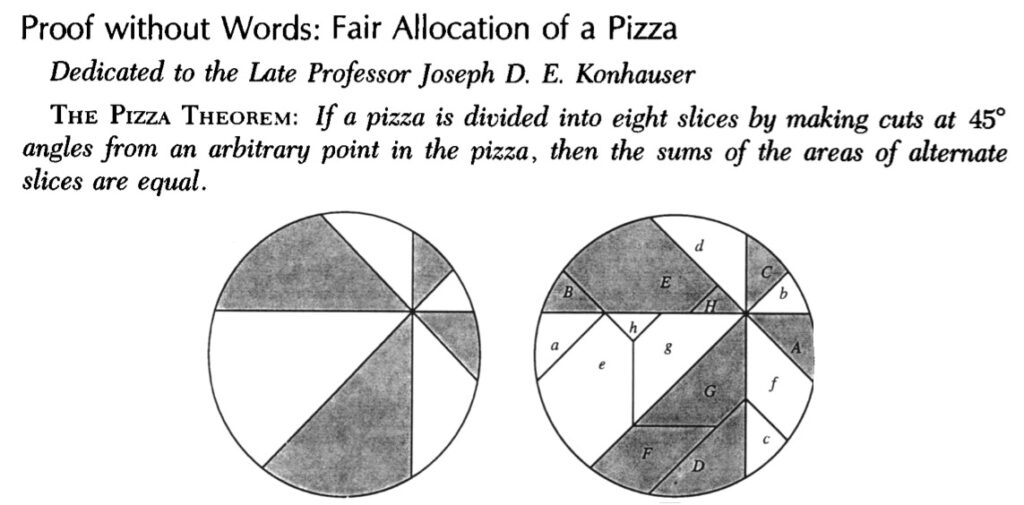
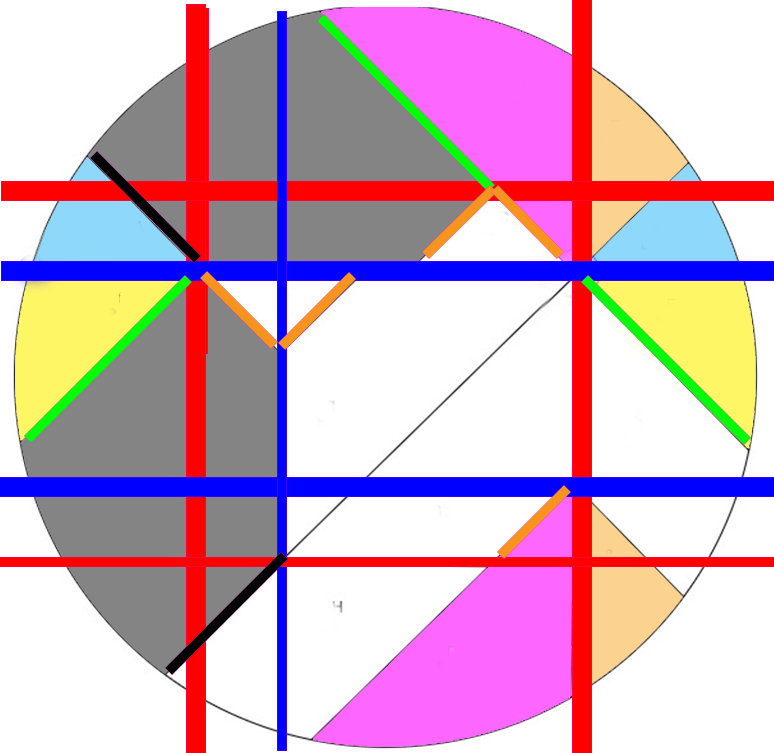
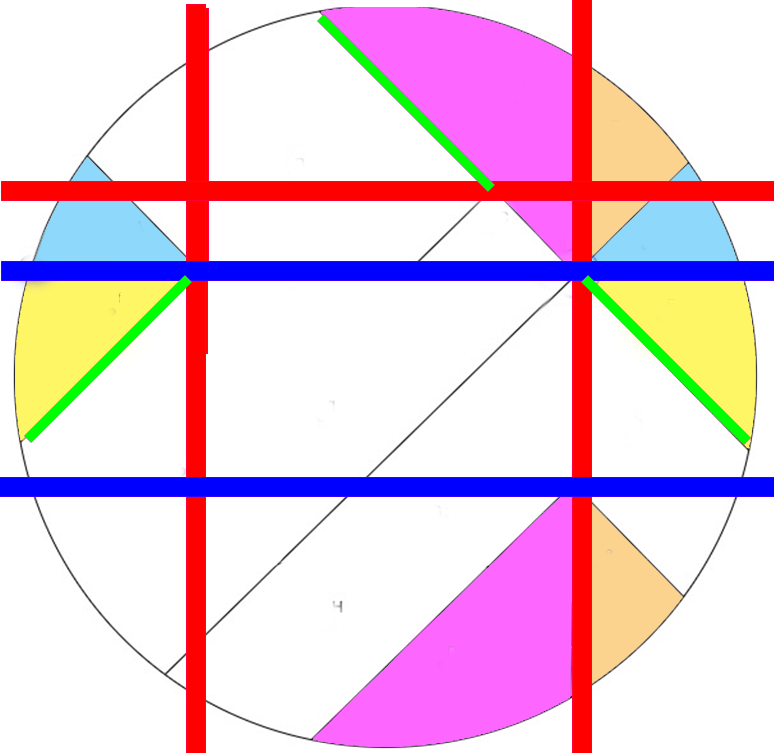
Un autre partage de pizza

Les parts ont toute la même forme mais non superposable.

Mais il y a mieux.

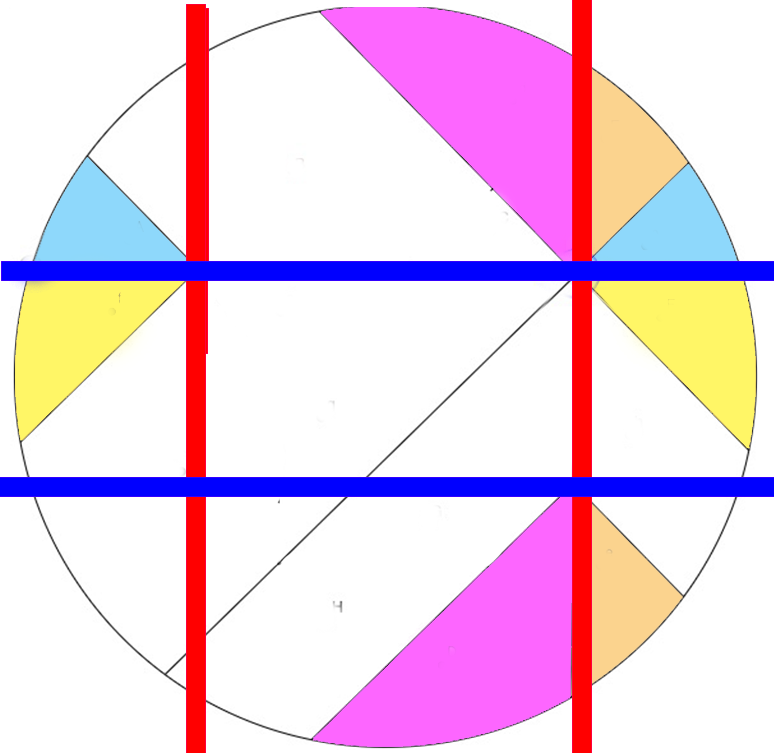
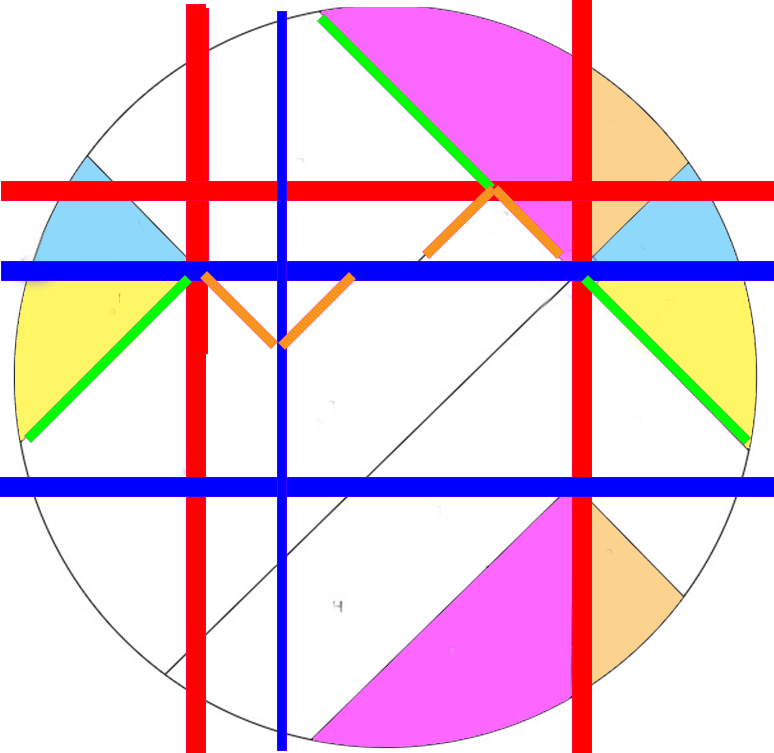
Un autre partage de pizza

Avantage:

Toutes les parts ont la même forme superposable

On peut choisir une part avec ou sans croute. Ou bien choisir une découpe où toutes les parts ont autant de croute.

On découpe 12 parts sans pour autant couper le center 12 fois

On peut recomposer une jolie forme même quand des morceaux ont été mangé.

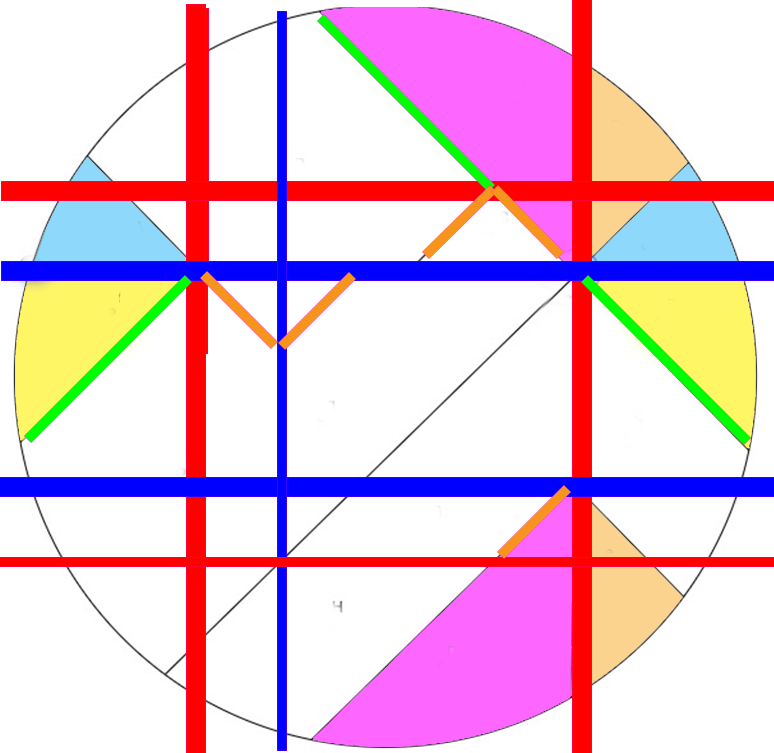
Pour des parts avec et sans croute, découper d’abord 6 parts avecla même courbure que le tour de la pizza.

Puis découper en deux chaque part ainsi:

Ci-dessous un autre réarrangement des même parts, mais dont on peut aussi obtenir le découpage dès le départ ainsi, et dans ce cas chaque part aurait autant de croute.

<div style='border: 2px solid #88AAAA; background: #DDFFFF; padding:8px;' ><img src="https://eva.louis-le-grand.net/maths/wp-content/uploads/2023/10/cuisine.png" alt="" class="wp-image-1120" width=30 /> <b>Conseil cuisine</b><br>
N’hésitez pas à utiliser des ciseaux pour découper vos pizzas. C’est la méthode préférée des Italiens qui vendent d’ailleurs les pizza au kilo. </div>

Conseil cuisine
N’hésitez pas à utiliser des ciseaux pour découper vos pizzas. C’est la méthode préférée des Italiens qui vendent d’ailleurs les pizza au kilo.

Conseil cuisine
Pour découper le bord de la pizza en 6, on peut soit faire une rosace avec un compas, soit plus simple :
– Marquez les points d’un diamètre.
– Imaginez la perpendiculaire à la moitié de la moitié du diamètre
– Marquez le bord atteint et recommencez pour les 3 points restants

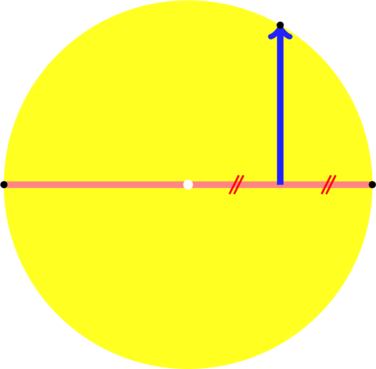
Résultat: