
Les gousses des grenades ont des losanges pour face, et voici pourquoi selon les explications de Kepler.
Prenons par exemple un cube comme modèle de gousse:
Un peu plus transparent:
Plusieurs comme plusieurs gousses qui vont grandir.
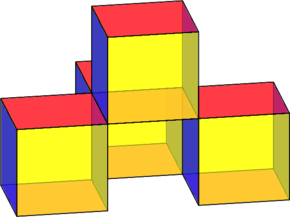
Faisons le gonfler, comme des baies sucrées qui se gorgeraient d’eau:
Gonflons les encore un peu plus:
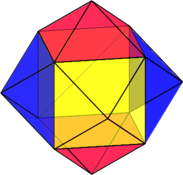
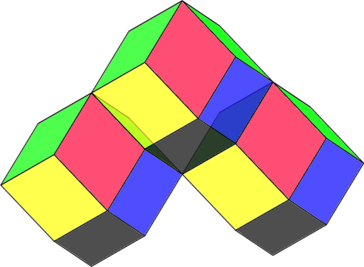
Tous en même temps:
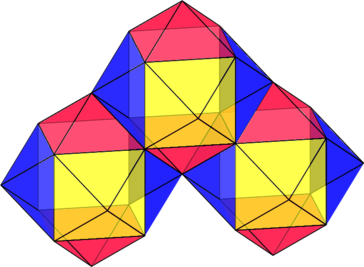
Il n’y a plus aucun espace libre. Les baies remplissent tout l’espace et pavent l’espace.
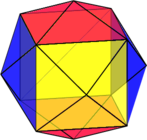
On remarque que des faces de la baie gonflée sont plates, on peut redessiner ainsi cette baie gonflée:

en la suivante en lui changeant juste les couleurs:
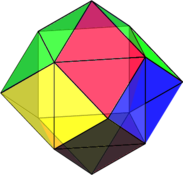
Et finalement:
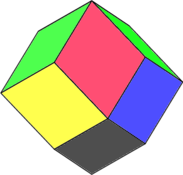
C’est un rhomboèdre: polyèdre à 12 faces losanges, et dont les gousses de la grenade ont la forme..
La grenade est le fruit du grenadier (Punica granatum)
Johannes Kepler offrit en cadeau à son protecteur Jean de Wacquenfels pour la nouvelle année 1611 : L’étrenne ou la neige sexangulaire.
Il y fait un lien entre mathématique et l’âme des aliments pour la première fois de l’humanité.


Porro si quis grandius aliquod malum granatum aperiat, videbit acinos plerosque in eandem figuram expressos, nisi quantum impedit series radicum, per quas alimentum illis suum suppeditatur.
Quaeritur iam in his duobus exemplis, quis sit auctor figurae rhombicae in alveolo apum inque granis mali punici. Materia in s causa non est. Nuspiam enim inveniunt apes huiusmodi foliola rhombica, in praeparato, quae colligant apes atque coaptent, ad e.ffigiandas suas domunculas. Neque verisimile est, in solis malis punicis sponte excrescere acinos in angulos, cum in omnibus aliis fructibus rotundi evadant, qua non impediuntur, humore suggesto 10 lentos cortices explente et referciente, ut turgescant, et, qua datur, protuberent.
Est igitur in acino quidem punici mali figurae causa in anima plantae, quae pomi procurat incrementum. Sed non est haec adaequata jigurae causa, neque enim hoc praestat fructui ex formali proprietate, sed adiuvatur necessitate materiali. Nam cum acini inter initia dum parvi sunt, rotundi sint, quamdiu spatium ipsis intra corticem sufficit, tandem indurescente cortice, crescentibus vero continue acinis, fit eorum constipatio et compressio, ut et pisorum intra suos oblongos calices. Sed pisa non habent quorsum cedant: oblongis enim siliquis ex ordine sunt inserta: comprimuntur igitur a duobus tcmtum lateribus. Acini vero rotundi in malis punicis uberius spatium a principio nacti, facile sese singuli intra ternos ordine adverso protuberantes insinuant, rotunditate sua adiuti, humoremque inde unde urgentur, declinantes in spatia vacua. Quod si quis aliquam vim globulorum rotundorum, interque sese aequalium ex materia molli constantium, concludat in rotundo vase illudque circulis aereis incipiat coarctare undique a plagis omnibus: globuli plurimi exprimentur in schema rhombicum: praesertim si prius illos globulos succussione vasis diligenti, locum angustiorem libero rotatu capere permiseris. Nam directa globulorum dispositione, quae turbari non possit, compressione Jacta cubas etiam eflicies.
In universum enim duobus modis inter se ordinantur globuli aequales in vase aliquo collecti, pro du obus modis ordinationis eorum in aliqua planifie.Et rursum tangetur unus globus ut prius, a duodecim aliis, a sex nempe circumstantibus in eodem piano tribus supra et tribus infra. lta in solida coaptatione arctissima non potest esse ordo triangularis sine quadrangulari, nec vicissim. P atet igitur, acinos punici mali, materiali necessitate concurrente cum rationibus incrementi acinorum, exprimi in figuram rhombici corporis: cum non infestis frontibus per 20 tinaciter nitantur rotundi ex adverso
acini, sed cedant expulsi, in spatia inter ternos vel quaternos oppositos interiecta.
Idem de malo punico intelligendum. Apparet necessitas materialis, 35 quae acinos perducit ad rhombicum, succedentibus incrementis. ltaque vanum est de essentia animae in hac arbore cogitare, quae rhombicum potissimum efficiat.
Encore, si l'on ouvre une grenade de taille plutôt importante, on verra que la plupart de ses gousses sont pressées dans la même forme, sauf en ce qui concerne le modèle de veines, par lesquelles leur nourriture est fournie, et qui les gênent.
Maintenant, la question se pose dans ces deux exemples : quel agent crée la forme rhomboïdale dans les cellules de la ruche et dans les gousses de la grenade ? Il ne peut s'agir de la matière en tant que cause. Car nulle part les abeilles ne trouvent des feuilles rhomboïdes de ce genre prêtes à collecter et à assembler pour la construction de leurs petites habitations ; et il est peu probable que les gousses de grenades seules se gonflent en angles, alors que dans tous les autres fruits, les baies se révèlent rondes, là où rien ne les gêne, car la sève montante remplit l'écorce résistante et souple et sa pression les fait gonfler - et même saillir là où l'écorce cède.
Ainsi, dans le cas de la gousse de la grenade, en tout cas, la cause de sa forme réside dans l'"âme" ou le principe vital de la plante, qui veille à la croissance de son fruit. Mais ce n'est pas une cause suffisante de sa forme : car ce n'est pas de par ses propriétés formelles qu'elle induit cette forme dans son fruit, mais elle est assistée par la nécessité matérielle. En effet, au début, lorsque les loges sont petites, elles sont rondes, tant qu'il y a suffisamment d'espace pour elles à l'intérieur de l'écorce. Mais plus tard, lorsque l'écorce durcit, tandis que les loges continuent de croître, elles se retrouvent serrées et comprimées, tout comme les pois le sont dans leurs gousses oblongues. Cependant, les pois n'ont pas de direction dans laquelle céder, car ils sont disposés en rangée à l'intérieur de leurs gousses oblongues : ils sont donc comprimés que sur deux côtés. Les gousses rondes des grenades, cependant, dès le départ, ont plus d'espace et s'installent facilement, chacune entre les trois qui enflent de la rangée opposée. Elles sont aidées par leur rondeur et dévient leur sève de l'endroit où elles sont soumises à une pression vers les espaces vides. Maintenant, si vous enfermez dans un récipient rond un certain nombre de petits pellets ronds de taille égale et de matière souple, et que vous commencez à le serrer de tous côtés avec des anneaux métalliques de tous les côtés, de nombreux pellets seront comprimés en une forme rhomboïdale, surtout si vous avez précédemment, en secouant soigneusement le récipient, encouragé ces pellets à rouler librement et à occuper un espace plus restreint. Si vous avez un motif de pellets à angle droit qui ne peut être perturbé, vous pourrez même obtenir des cubes en appliquant une pression.
En général, des pellets égaux, lorsqu'ils sont rassemblés dans un récipient, s'organisent mutuellement de deux manières en fonction des deux modes de les organiser dans un plan.Cependant, bien que dans cette construction, chacun dans une couche supérieure soit assis entre trois dans la couche inférieure, si vous tournez la figure de manière à ce que ce ne soit pas le sommet mais un côté entier de la pyramide qui soit en haut, vous trouverez que chaque fois que vous retirez une boule du sommet, quatre autres se trouvent en dessous d'elle dans un motif carré. Encore une fois, comme précédemment, une boule sera touchée par douze autres, à savoir, par six voisins dans le même plan, et par trois au-dessus et trois en dessous. Ainsi, dans l'emballage le plus serré en trois dimensions, le motif triangulaire ne peut pas exister sans le carré, et vice versa. Il est donc évident que les gousses de la grenade sont comprimés dans la forme d'un rhomboïde solide : les exigences de leur matière coïncident avec les proportions de leur croissance. Les locules globulaires opposés les uns aux autres ne persistent pas à se pousser mutuellement face à face, mais sont déplacés et glissent sur le côté dans les espaces laissés entre trois ou quatre autres dans le plan de confrontation.La grenade doit être comprise de la même manière. Une nécessité matérielle qui guide les gousses vers le rhomboïde à mesure que la croissance suit la croissance, est apparue. Il est donc superflu de penser au principe intérieur de l'âme de cet arbre qui le dirige vers la préférence du rhomboïde.Même constat pour les oeufs de saumon bien compressés les uns aux autres.


| André Deledicq , Le cadeau de Kepler, Edition Kangourou |  |
Attention, il existe un autre Rhombic dodécaèdre (polyèdre à 12 faces losanges). Voici une nouvelle fois celui que connait Kepler:
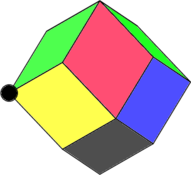
Et celui que ne connaissait pas Kepler découvert en 1960 par Bilinski. Il a le grand axe des losanges gris tournés de 90°. Globalement ce Losange-polyèdre-à-12-faces est plus aplati que le précédent, mais il pave aussi l’espace.
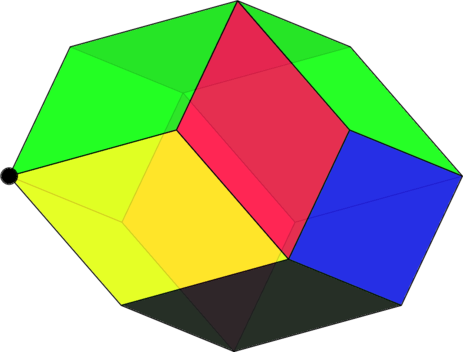
Losanges dans le polyèdre de Kepler:

Rapport des longueurs des diagonales: ![]()
Losanges dans l’autre polyèdre:

Rapport des longueurs des diagonales: ![]()

Les abeilles?
Comme la pression osmotique pousse dans les grenade, les abeilles créent des alvéoles rhombiques. Ce n’est pas le fruit d’un calcule intelligent des abeilles, mais juste le résultats des mathématiques.
