Des gâteaux irréversibles

Les préparations culinaires sont-elles réversibles ? Peut-on défaire un mélange ? décuire un gateau ? De l’irréversibilité du monde et de la croissance de l’entropie.

Prenons 100 M&M’S de 5 couleurs.

Prenons un bol avec 100 M&M’S et mélangeons.

VIEDO A INSERER ICI

Surprenant n’est-ce pas ?

Calculons combien de positions ordonnées existe-t-il de 5 paquets de 20 M&M’S

C(20 parmis 100) = n! / (20 ! * 80!) = 10^20

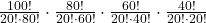
Cela fait un nombre à 67 chiffres: 1094915415525119820987225688309818220883072063883928031640993360000

Il serait déjà remarquable qu’un ensemble d’une seule couleur soit regroupée. cela représente alors une chance sur 107196674080761936594. En effet si on impose parmi les combinaisons possible qu’une des 5 couleurs soit regroupée à n’importe quelle des 100 positions du carré possible, il reste encore un grand nombre de combinaisons:

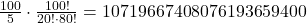
Si l’on teste 10 de ces positions par seconde, il faudrait …

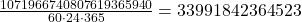
… plus de 30 000 milliards d’années, 2 000 fois l’âge de l’univers.

Boltzman a modélisé l’entropie, c’est-à-dire une mesure du désordre, qui ne peut que augmenter dans l’univers.

Voici 100 M&Ms. Toutes les secondes, 10 couples de M&M’S sont échangés.

Modèle sans corrélation: des paires de M&Ms sont échangées. Le système est irréversible:

(lancer le modèle ci-dessous)

En à peine quelques secondes, tout semble bien mélangé irrémédiablement. Il faudrait des millions d’années pour avoir la chance de retomber sur la situation de départ ! Le désordre (c’est-à-dire l’entropie) a augmenté.

Modèle avec corrélation: les paires de M&M’S sont échangées mais pas indépendamment. Le système est irréel:

(lancer le modèle ci dessous, et patienter un peu …)

Cette fois, il n’y a pas d’information perdue. Même si au bout de quelques secondes tout semble aussi mélangé, on se souvient quelles paires ont été échangées successivement. Et au bout d’une trentaine de secondes, on peut revenir à une situation bien rangée. Et cela doit surprendre.