Un gâteau catégorique

Si vous n’avez jamais entendu parler de la théorie des catégories en maths, c’est pourtant un des 50 domaines mathématiques listés par la Maison Poincaré à Paris.

C’est l’art de modéliser de la meme manière des objets très différents.
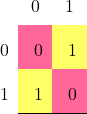
Regardez ce tableau .

C’est la règle d‘additionon en binaire .

0+0=0
1+0=1
0+1=0
1+1=0 et il y a une retenue de 1

ce qui donne sous forme de tableau:

C’est aussi la table pour la règle de signe quand on multiplie deux nombres ensemble et qu’un veut connaître le signe du résultat.
+ x + = +
+ x – = –
– x + = –
– x – = +
et que l’on peut représenter par un même tableau.

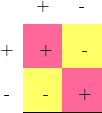
Ou encore la règle complexe::

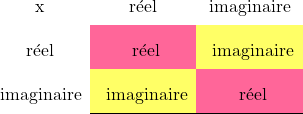
Ou encore le tableau de multiplication:

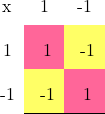
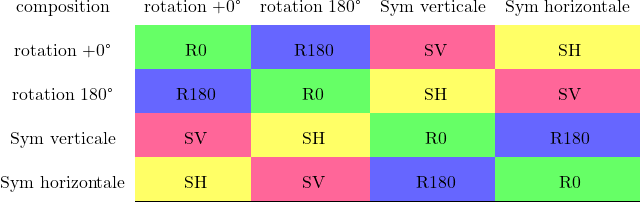
Ou encore le tableau de composition de rotations:

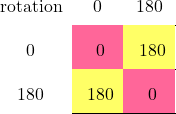
Voici maintenant un tableau plus grand:

Cela peut représenter à la fois la multiplication modulo 8 des nombres impairs:

Ou encore la table de composition des isométries du rectangle:

Les isométries du rectangle, sont les transformations qui laissent inchangées le rectangle.

%Rectangle

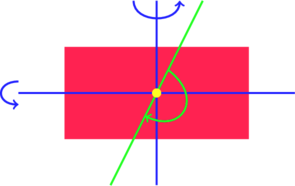
Ce sont les rotations d’angle 0° (identité) ou d’angle 180°, et les symétries horizontales ou verticales. Puis on établit la table de composition de ces transformations.

%R0: rotation 0°

%R180: rotation 180°

%SV: symétrie verticale

%SH: symétrie horizontale

Ou encore ce gâteau:

Conseil cuisine
Cuire quatre quatre quarts séparément. Etaler de la confiture entre les morceaux. Etaler de la pâte d’amande entre 2 feuilles de papier sulfurisé.

Lecture

Ce lien entre la théorie des catégories en mathématiques et le gâteau de Battenberg itératif est inspiré du livre d’Eugenia Cheng: Comment cuire un neuf.