
Notre pâte contient de l’eau et de la levure chimique ou boulangère.
Au four, l’eau s’évapore (il fait plus de 100°C) et crée des bulles de gaz dans la pâte.
La levure de boulangerie est faote de petits organismes vivants qui mangent le sucre de la pâte et fait produit comme déchet du ![]() , ce qui forme aussi des bulles.
, ce qui forme aussi des bulles.
La levure chimique est du Carbonate de Calcium ![]() en poudre qui produit aussi du
en poudre qui produit aussi du ![]() en milieu légèrement acide et donc des bulles dans la pâte.
en milieu légèrement acide et donc des bulles dans la pâte.
Voici notre pâte au début avec des petites bulles. Disons qu’il y ait 33% de bulles un peu plus grosses que les autres aléatoirement réparties, ainsi:


Les bulles grossissent au cours de la cuisson puis le gâteau est complètement cuit et dur et les bulles n’évoluent plus. Voici le résultat:

On remarque qu’il s’est formée des bulles géantes de taille caractéristique 4.
Ce gâteau reste imperméable car il n’y a pas de communication des bulles à grande échelle.
Reprenons notre recette en y mettant plus de levure. Cette fois le temps d’enfourner le gâteau, non plus 33% des bulles sont déjà de taille moyenne, mais 50%.

Puis elles grossissent jusqu’à la fin de la cuisson:
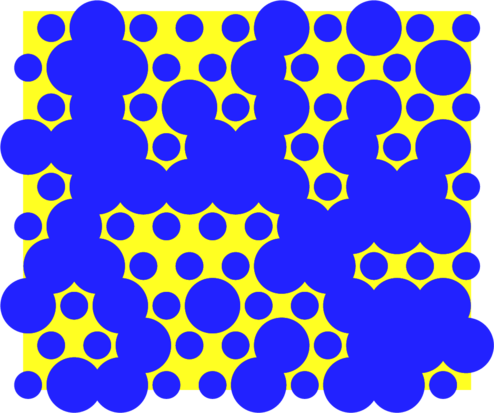
Cette fois, il y a une bulle géante qui communique dans tout le gâteau.
On dit qu’il y a eu percolation. Notre gâteau n’est plus imperméable et le lait peut s’imbiber à la place des bulles dans tout le gâteau.
Quelle quantité de bulles permet la percolation ?
Quand a lieu la percolation on a une bulle géante aussi grosse que le gâteau. Avant que cela n’arrive, quand on a pas assez de bulles, à la fin de la cuisson, on a des grosses bulles, de taille 4 par exemple sur notre premier exemple.
Changeons d’échelle, et regardons notre gâteau de plus loin.
Dans notre premier cas (avec 33% de grosses bulles), on peut regarder de 2 fois plus loin, et nos grosses bulles de taille 4 apparaitront comme grosses bulles de taille 2. Si on regarde de 4 fois plus loin, les plus grosses bulles de taille 4 apparaitront comme des grosses bulles de taille 1. Mais on ne peut pas regarder de plus loin, sans quoi on ne verra plus de bulles du tout.
Dans notre second cas (avec 50% de grosses bulles), c’est différent. D’aussi loin qu’on regardera le gâteau, on verra toujours une grosse bulle géante aussi grosse que le gâteau tout entier. Au seuil de percolation, il n’y a plus de taille caractéristique. Le gâteau est auto-similaire à toute échelle.
Fixer une échelle, on appelle cela la normalisation. C’est à dire qu’on pose une norme, un longueur caractéristique, une unité. Si on change de norme, en changeant d’échelle c’est la renormalisation. Mais si on peut changer de norme tout en laissant le problème est inchangé pour la caractéristique observée, alors on peut dit qu’on peut renormaliser et qu’on a un invariant par renormalisation.
Modélisation de la renormalisation
Disons que chaque bulle a une probabilité ![]() d’être petite et
d’être petite et ![]() d’être grosse au début.
d’être grosse au début.
Voici les 8 cas de bulles à proximité suivant que chaque bulle peut être petite ou grosse, la probabilité de l’arrangement, et par quoi on peut remplacer l’arrangement si on s’éloigne par renormalisation.

En regroupant et en ajoutant les probabilité ci-dessus, la probabilité d’avoir une petite bulle qui ne connecte pas est de ![]() . Et ce doit être la probabilité
. Et ce doit être la probabilité ![]() d’avoir une petite bulle au départ lorsqu’on est au seuil avec une composante géante car on peut renormaliser sans rien changer. D’où à la probabilité critique de seuil:
d’avoir une petite bulle au départ lorsqu’on est au seuil avec une composante géante car on peut renormaliser sans rien changer. D’où à la probabilité critique de seuil:
![]()
On a donc un seuil à ![]() nous indiquant combien de bulles on doit avoir pour que notre gâteau soit spongieux. En dessous de ce seuil il sera imperméable, au dessus, il s’imbibera car le lait remplira la bulle géante.
nous indiquant combien de bulles on doit avoir pour que notre gâteau soit spongieux. En dessous de ce seuil il sera imperméable, au dessus, il s’imbibera car le lait remplira la bulle géante.
Simulations

Simulation pour montrer le seuil brutal très précis de 50% dans ce modèle. Recharger la page pour de nouveaux tirage au sort.
40% des bulles sont grosses. On a pas de percolation; le gâteau est imperméable; les plus grosses bulles ne réunissent qu’une 20aine de bulles, la longueur de corrélation est de 20. Au delà de la distance de corrélation, du lait dans remplissant une bulle n’impliquera pas du lait ailleurs. :
45% des bulles sont grosses. On a pas de percolation; le gâteau est imperméable; les plus grosses bulles ne réunissent qu’une 40aine de bulles; la longueur de corrélation est de 40:
50% des bulles sont grosses. La corrélation est infinie: du lait quelque part impliquera du lait dans tout le gâteau:
55% des bulles sont grosses. Les bulles sont quasi toutes jointives
Séparer 3 jaunes (petit bol) et blancs d’oeuf (grand bol)
Mettre 1gr de sel sur les jaunes d’oeuf et 2ml d’extrait de vanille puis mélanger
Faire une meringue — Monter en neige les blancs d’oeuf en ajoutant 3x30gr de sucre en poudre ! Fouetter jusqu’à ce que ça tienne et forme des pics.
Incorporer les jaunes d’oeuf dans le grand bol et mélanger soigneusement avec l’appareil
Ajouter 90 gr de farine ordinaire, incorporer/mélanger de bas en haut (doucement)
Dans un récipient moyen, mettre 30gr d’huile végétale et de lait à température ambiante et y mélanger avec un peu de pâte à gâteau
Mélanger les deux préparations doucement en faisant des cercles
Mettre dans la casserole et frapper pour enlever les bulles d’air
Mettre au four à 170 degrés pendant 30 min (chaleur tournante)
