L’intro de l’IA: Bienvenue dans le monde enchanté où les gâteaux deviennent des chefs-d’œuvre photolélastiavecques et biréfringents ! Ce chapitre sucré nous transporte dans une aventure où la pression extérieure transforme les desserts en prodiges optiques. Chaque cuillère devient une baguette magique, ajoutant des tensions et des décalages pour composer un festival de couleurs. Les gâteaux deviennent des toiles de biréfringence, où les décalages colorés entre composantes créent une danse cosmique de polarisation. Ces délices, équations gourmandes, révèlent des retards qui correspondent à des déphasages délicieusement colorés. 🍰🎨
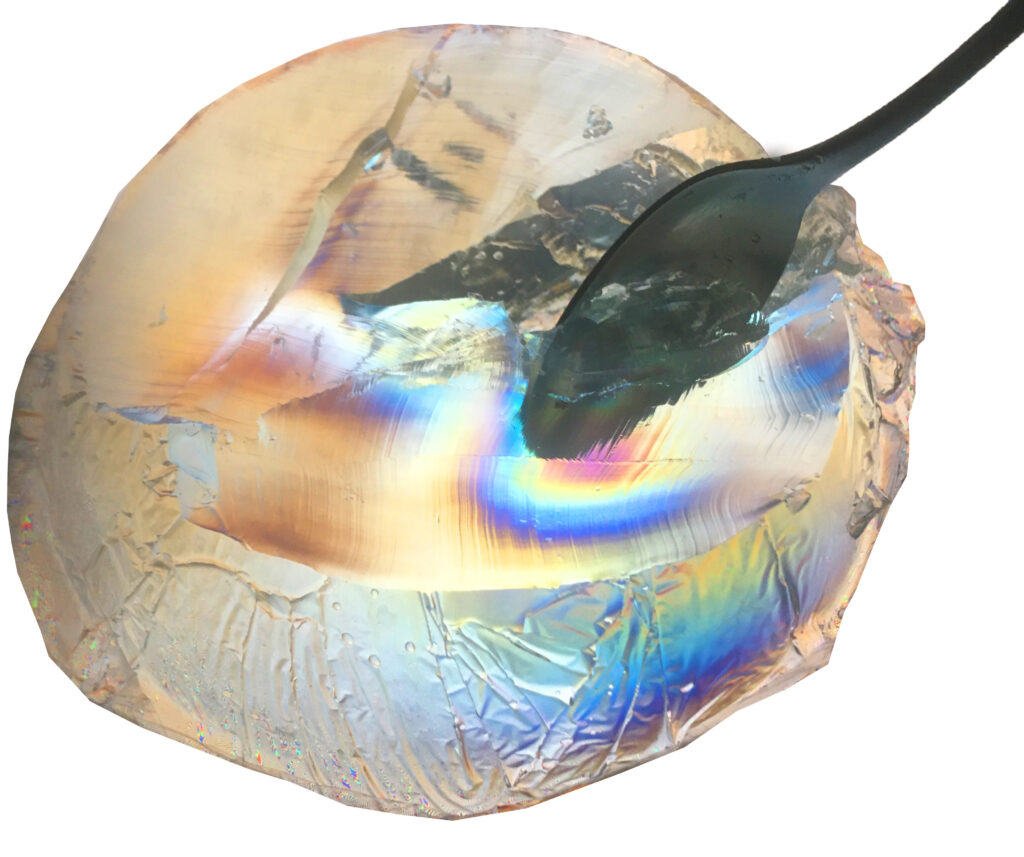
L’effet photoélastique: le gâteau devient biréfringent sous l’effet d’une contrainte extérieure de pression.


Milieu isotrope: voici une particule du gateau qui va être excitée par la lumière. Elle est reliée au réseau des autres particules qui l’entourent par des liaisons modélisées par des ressorts ici:
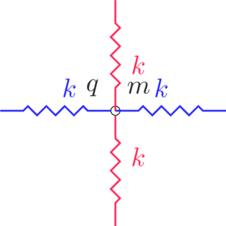
Lorsqu’on appuie avec la cuillère dans une direction, on ajoute une tension dans une direction.
Milieu anisotrope
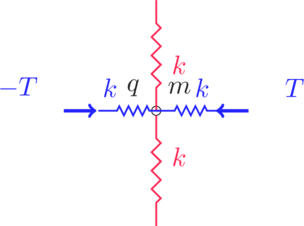
Les deux oscillateurs n’ont plus les même caractéristiques suivant les vibrations dans une direction (verticale) ou l’autre (horizontale).
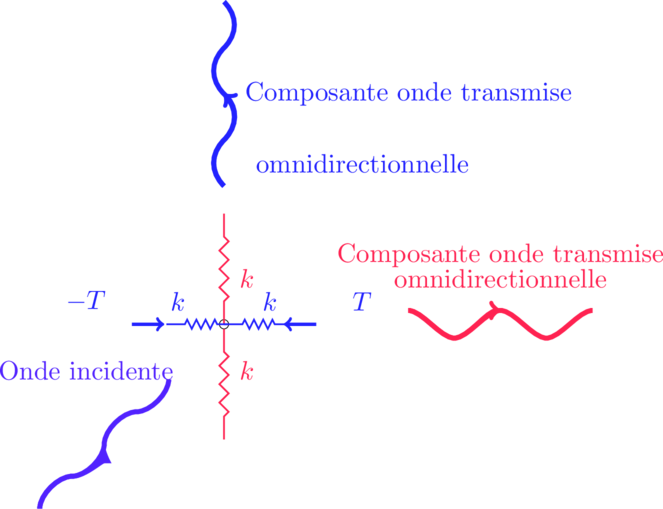
L’onde électrique ![]() arrive sur la particule:
arrive sur la particule: ![]() . La particule est excitée avec la pulsation
. La particule est excitée avec la pulsation ![]() de la lumière qui lui arrive dessus pour une certaine couleur de lumière. Elle va donc vibrer avec un régime forcé à la pulsation imposée
de la lumière qui lui arrive dessus pour une certaine couleur de lumière. Elle va donc vibrer avec un régime forcé à la pulsation imposée ![]() . Par contre son amplitude et sa phase dépendent des caractéristiques de l’oscillateur
. Par contre son amplitude et sa phase dépendent des caractéristiques de l’oscillateur ![]() On va donc avoir une onde transmise qui se décompose suivant les axes en
On va donc avoir une onde transmise qui se décompose suivant les axes en ![]() et
et ![]() ainsi:
ainsi:
Comme suivant un axe et l’autre on a un déphasage ![]() et
et ![]() , on a donc un retard entre une des deux composantes par rapport à l’autre.
, on a donc un retard entre une des deux composantes par rapport à l’autre.
Le retard entre les deux composantes de l’onde correspond à un déphasage qui dépend de la longueur d’onde, c’est-à-dire de la couleur.


Conséquences sur le plan de polarisation
Voyons quel est l’effet du retard entre les composantes de même fréquence d’une onde polarisée selon un axe.
Si les deux composantes suivant 2 plans orthogonaux sont tout d’abord en phase:
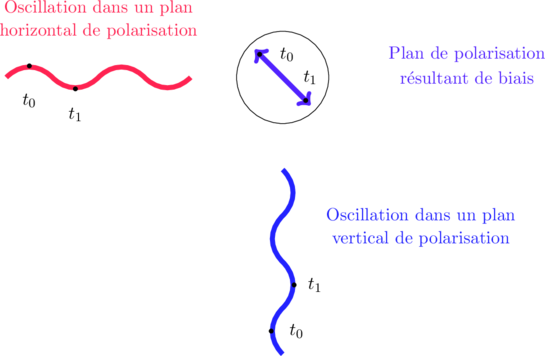
A présent, ajoutons un retard à la composante dans le plan rose par rapport à la composante dans le plan bleu (l’indice et donc la vitesse de l’onde suivant une direction étant différente de l’autre plan):

Le retard dans un plan a eu pour conséquence de modifier l’amplitude de l’onde dans le plan de polarisation observé.
Avec un décallage plus important entre les 2 plans, de ![]() , on a :
, on a :
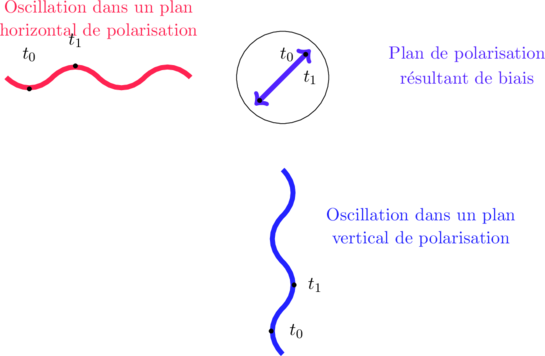
On a fait tourner le plan de polarisation de ![]() .
.
Conséquences sur les couleurs

La modification d’amplitude dépendante de la longueur d’onde, c’est pourquoi les images obtenues avec de la lumière blanche présentent des irisations colorées.
On peut calculer suivant le retard d’un plan par rapport à l’autre, quelles couleurs vont être atténuées et quelle sera la couleur résultante visible et comparer à ce qui est observé.
Pour une longueur d’onde donnée, l’intensité de la couleur observée est donc suite à l’interférence d’une onde avec la même suivant un autre axe se propageant à une vitesse différente:
![]()
![]() et
et ![]() révèlent les contraintes.
révèlent les contraintes.

Modèle:
Observé:

Ce qui correspond bien à ce qui est observé.
Isostatiques, Isochromes
Quand on appuie au milieu, on observe une croix ainsi avec deux branches bleues et deux rouges:


Les lignes isochromes, ces lignes d’égal cisaillement On peut aussi regarder la forme des isoclines. dépendent de l’intensité de la charge appliquée et de la longueur d’onde utilisée. Le long des isochromes, la différence de chemin optique est égale à un nombre entier de fois la longueur d’onde. Ces lignes s’appellent isochromes, car observées en lumière blanche (spectre large). Ce sont des lignes d’égale couleur.
- Ne se croisent pas sauf aux points d’isotropie (ici le centre où on appuie)
- Donnent l’orientation des contraintes
- principales dans tout le corps
- Servent à tracer les isostatiques (lignes de
force perpendiculaires aux isoclines)
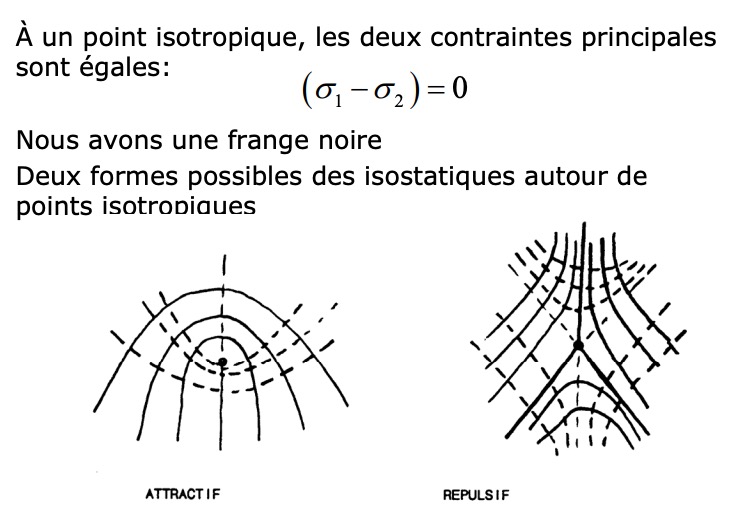
Ce qu’on observe , ou pas ?

Julien Fade à l’Espace des sciences de Rennes:
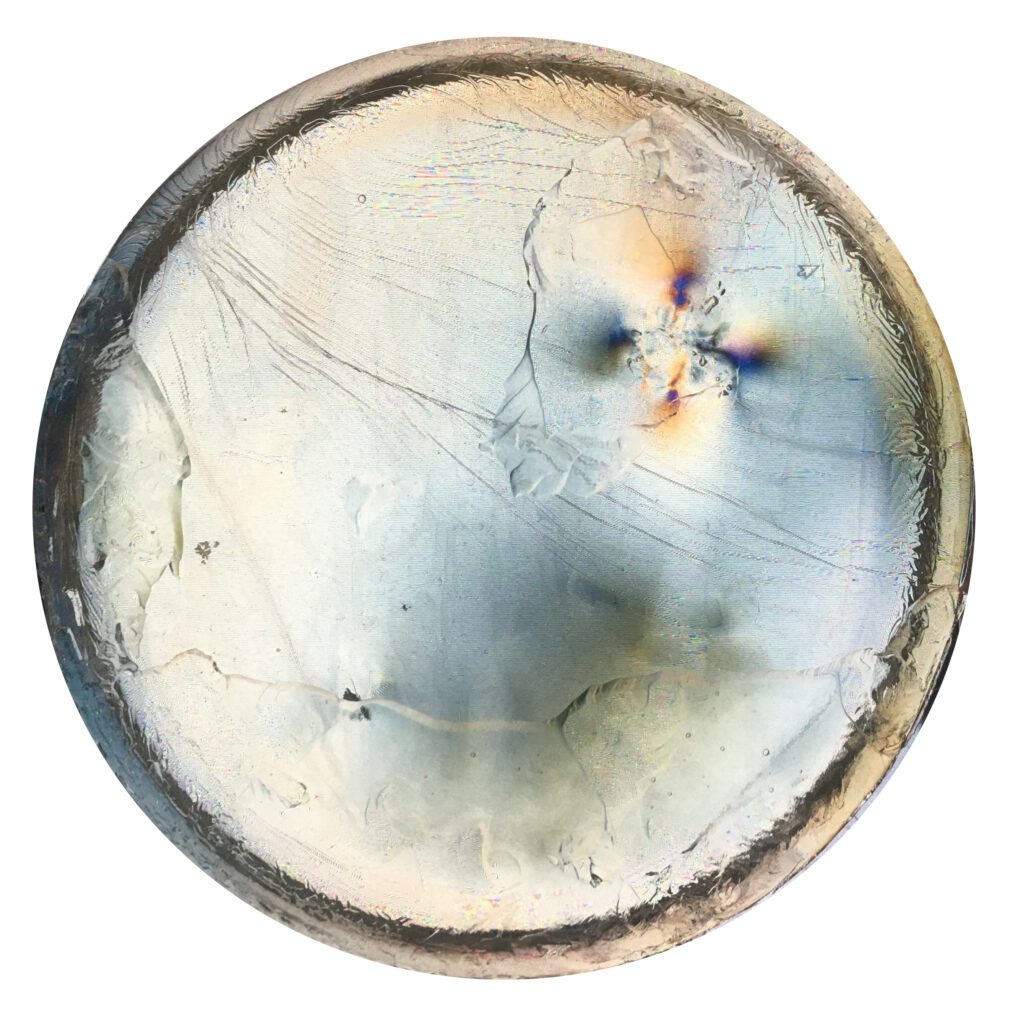
Tarte au citron transparente avec une fève
c’est l’époque de la galette des rois, et jaloux des gâteaux mathématiques, mon professeur de physique a voulu un gâteau physique.
Comment cacher une fève dans un gâteau transparent ?
La tarte au citron parait uniforme au premier regard.

Pourtant en lumière polarisée, les précontraintes introduites apparaissent. Pour réaliser la fève en contrainte, un trou a été réalisé dans le gâteau. Puis le trou a été bouché par un bouchon d’une taille supérieur au trou, inséré avec force dans le trou pour contraindre localement la tarte. Puis un peu de gélatine est à nouveau coulée pour cacher les jonctions et rendre la surface supérieure bien lisse.
En lumière polarisée, voici ce qu’on observe, et on localise bien la fève sans ambiguité:
Il ne reste plus qu’à dresser le gateau en posant la couche au citron sur un tarte en pâte brisée, et rajouter de la meringue sur le dessus pour avoir notre tarte au citron transparente meringuée.

Recette: Gélatine 2 à 4 paquets pour 1L environ, acide citrique 50g pour 1L environ, sucre à convenance environ 150g/Litre, Eau (1L). Merinque: blanc d’oeuf en neige puis ajouter le sucre, au four 1h à 120°C.

