
Voici un vélo.
Il fait le tour de la maison et revient au point de départ.
Le soleil est au zénith. Quelle est l’aire balayée par l’ombre sous le vélo ?
On considère que la roue avant ne croise jamais l’axe de la roue arrière. La distance entre les 2 roues du vélo est appelée R.
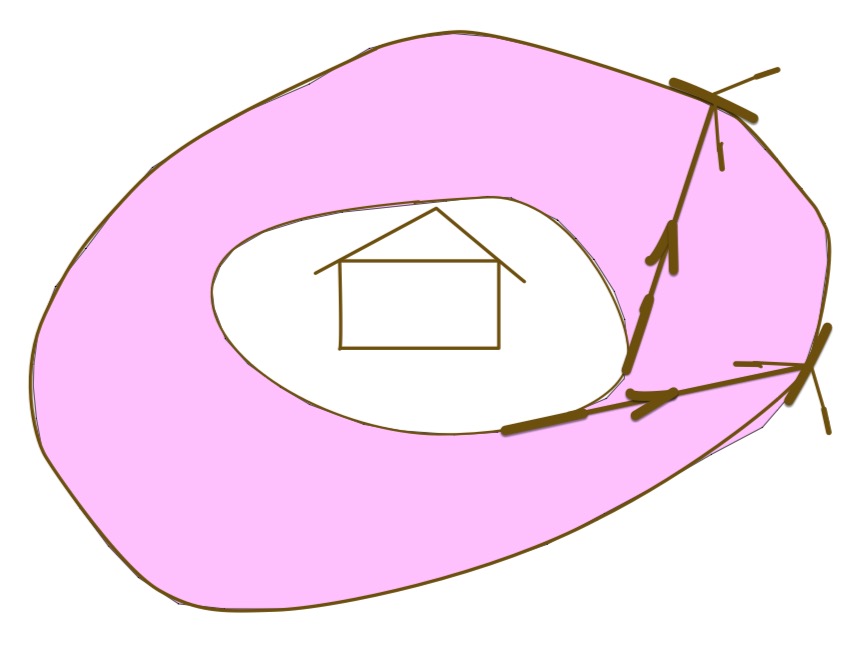
L’aire est le même que ce vélo fasse le tour d’une maison ou de la ville toute entière.
C’est la même aire que si le vélo reste sur place sans bouger la roue arrière et fait un tour sur lui même. C’est la surface de ce gâteau. Pi.R^2.
La roue arrière est tangente au bord intérieur de l’ombre. Au cours d’un petit déplacement, le segment du cadre du vélo se déplace sur un triangle d’aire r.dtheta. Seule la contribution du déplacement perpendiculaire au cadre compte. La contribution du déplacement dans l’axe du cadre ne contribue pas à l’aire de l’ombre balayée. Au bout d’un tour, l’angle a fait 360°. L’aire balayée est donc pi.R^2.
Autrement dit si on supprime la composante axiale du cadre de la vitesse, le vélo ne fait que parcourir en rond le disque de rayon R.
Cycloïde
Toujours sur notre vélo, suivons à présent le trajet de la valve de la roue lorsque le vélo avance d’un tour de roue. Cette courbe est appelée cycloïde et l’on cherche l’aire sous cette courbe, en rose.
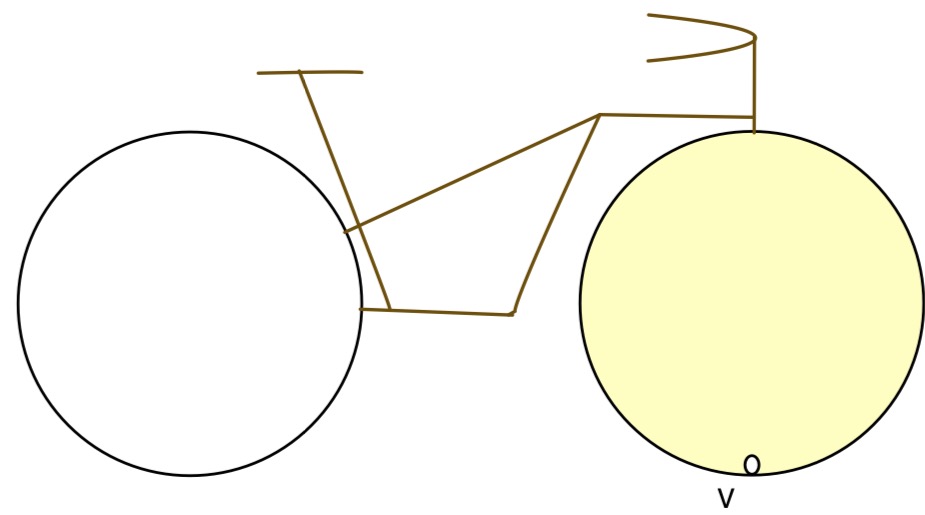
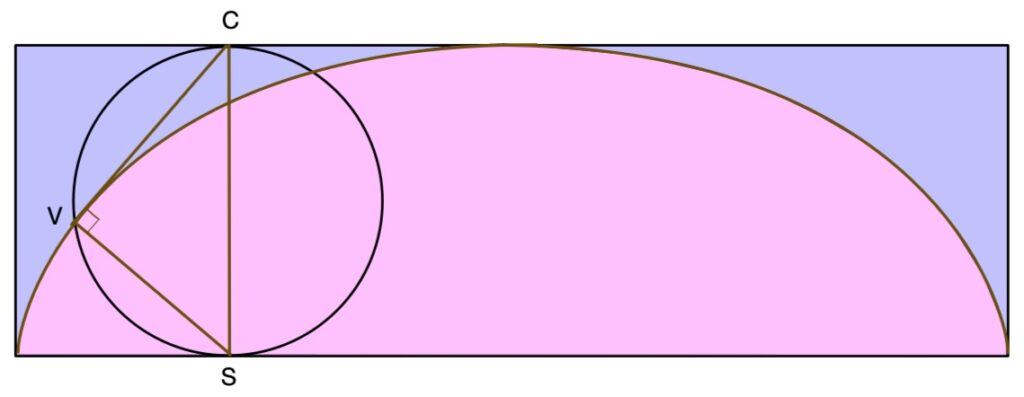
Le rectangle bleu a pour hauteur 2.R et pour longueur le périmètre de la roue: 2.pi.R. Donc la surface du rectangle est 4.pi.R^2, soit 4 fois la surface de la roue (pi.R^2).
Cherchons à présent l’aire bleu au dessus de la cycloïde.
Intéressons nous au segment [VC].
S est le point de contact avec le sol. V la valve. A chaque instant la roue tourne autour de S. Donc V de déplace perpendiculairement à VS puisque V à tendance à tourner en rond autour de S. Donc VS est perpendiculaire à la tangente à la cycloïde en V. Comme on a un angle droit en V avec la tangente, la tangente coupe donc le cercle au point diamétralement opposé à S tout en haut: C.
Que parcourt le segment [VC] au cours du mouvement ? [VC] se déplace selon son axe et tourne de 180° en parcourant un disque. L’aire balayée par [VC] est donc la surface de la roue, et c’esr l’aire bleue.
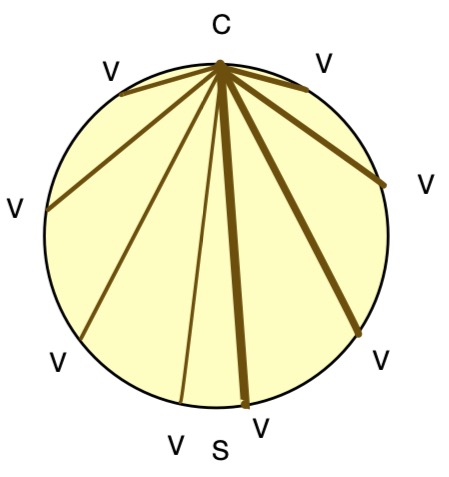
On soustrayant d’aire bleu à celle du rectangle on a donc que l’aire ros est de 3 roues: 3.pi.R^2
