Quand on tourne la lame, elle tourne et se déplace plus vite sur le bord qu’au centre. Donc plus d’énergie est apportée sur le bord 
croissant avec le carré de r. La tranche de fromage s’y allonge plus qu’au centre. Le périmètre normalement de 
, est supérieur. Cela forme une fleur.
Dimension fractale d’une tranche de fromage, compris entre 1 et 2.
Mot clé: Flambage. et Morphogenèse et auto-organisation: tiges, plaques, films et gouttes.
La tranche de fromage à pour dimension: 2,5849625..
A chaque étape ci-dessous on utilise un segments de longueur de la moitié du précédent. Et il faut 3 segments deux fois plus courts pour mesurer le tour de la tranche, là où on s’attendait à doubler le nombre de segments quand on en divise la longueur par deux. Et on peut itérer 6 fois le procédé ! A chaque étape, la courbe est mieux approchée avec des segments deux fois plus courts, mais pourtant il y a toujours des bouts qui dépassent.
Pour un segment de longueur 1 unité. Si on le mesure avec des segments de longueur 2 fois plus petits, il faudra 2 segements pour mesurer le segment initial.
Pour un carré en 2 dimensions, si on prend un carré 2 fois plus grand que le carré unité, il faudra 
petits carrés unités pour mesurer le grand carré de coté 2.
Pour un cube de coté 2, il faut cette fois 8 petits cubes unités pour le mesurer.
A chaque fois il pour un objet 2 fois plus grand, il faut 
.
Mais pour le tour de notre tranche de fromage, il faut 3 fois plus de segments quand on en divise la taille par deux.
au lieu de 
, 
, 
le facteur est de 3. Mais 3 c’est 
on calcule: 
en prenant le logarithme 
soit avec la propriété du log: 
et finalement 
Le pourtour de la transche de fromage n’est pas de dimension 1 mais de dimension 1,58 environ. Et la tranche complète avec sa profondeur en plus apporte 1 dimension supplémentaire, soit finalement, là où on croyait avoir une tranche de fromage de 2 dimension, elle a pour dimension 2,58…. !
D’ailleurs on peut remarquer en effet q’une seule coordonnée ne suffit pas pour positionner un point sur le pourtour de la tranche de fromage. Par exemple si on indique un point à 3cm de l’origine sur le pourtour, on ne trouvera pas le même point suivant l’unité utilisée. Et plus l’unité utilisée sera petite, plus le point se trouvera près de l’origine.
Position d’un point à la distance 2 sur un cercle, suivant l’échelle utilisée:
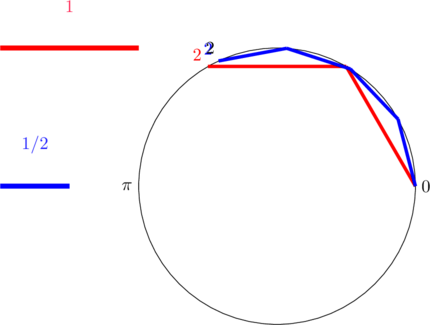
Le point converge très vite vers le point à la distance 2 en noir sur la courbe. Mais sur le tour de tranche de fromage:
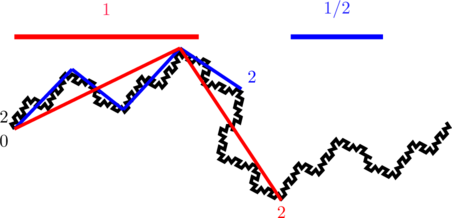
Plus on prend une petite échelle, plus on se rapproche de 0. Une coordonnée ne suffit plus car on est à plus que une dimension. Presque à 2 dimensions.
Voici une alternative locale française à la Tête de Moine suisse et qui fonctionne tout aussi bien pour faire de belles tranches (photos des tranches ci-dessus).
Salade frisée
Les feuilles de salades ont le bord plus long que si elles étaient plates. Ce qui s’explique par la croissance plus importante des cellules de bord. Ce phénotype est sélectionné car il donne du volume à une feuille qui serait autrement platte et les feuilles s’empileraient dans l’assiette.
Les feuilles de salades ont le bord plus long que si elles étaient plates. Ce qui s’explique par la croissance plus importante des cellules de bord. Ce phénotype est sélectionné car il donne du volume à une feuille qui serait autrement platte et les feuilles s’empileraient dans l’assiette.
Les feuilles de chou frisées sont particulièrement remarquable. En voici une crue et une cuite.
Même cuite la feuille garde sa 2,5ème dimension. On peut la frire ensuite, et cela donne des chips en 3d qui ne s’aplatissent pas du tout, et qui sont bons et croustillants. Le résultat, bien que un peu huileux, est entre la pkaïla (plat tunisien à base de feuilles d’épinard frittes mais qui perdent toutes leurs dimensions lors de la cuisson et qui sont réduites à quelques points dans une bain d’huile avec quelques haricots) et les feuilles de nori japonaises croustillantes mais qui sont plates à moins de les plier comme des origami.
Feuille de nori froissée comme pâle imitation qui reste plat.
Pkaïla comme autre pâle imitation mais le croustillant et les dimensions sont perdues.
L’avantage de la dimension supérieure du chou frisé, c’est sa bien plus grande surface. La surface c’est ce qui est contact avec la sauce et l’assaisonnement. Donc plus de surface signifie plus de sauce. Et aussi plus de contact avec les papilles en bouche.
Chocolat
Faire fondre le chocolat au bain marie, puis lui donner la forme du cylindre avec un axe creux.
Utiliser un axe rigide directement pris dans le chocolat est une mauvaise idée car il restera solidaire du chocolat et sera impossible à retirer. Dans ce cas, mieux vaut l’entourer d’une couche de papier sulfurisé dont il sera amène de glisser.
Le chocolat est trop cassant et non plastique. L’énergie sur la périphérie du cylindre engendre une multitude de craquelures, et cela n’a pas pour effet d’allonger le chocolat déjà très fin. On obtient pas de rosette de chocolat mais de simple copeaux en forme de cône. Il faudrait un chocolat plus plastique. Peut être faudrai-il lui ajouter .. du sucre ?.
Jupes
C’est aussi le cas des jupes à godet réalisées à partir d’un patron en forme de portion de cône.
La ceinture est représentée en noir.
Mieux encore, on trouve des habits tricotés hyperboliques mais c’est une autre histoire.
Conseil cuisineLa girolle fonctionne avec la Tête de Moine, le Ptit Basque, la Tome, le chocolat.
Une métrique 
qui traduit l’allongement du bord d’un facteur 
dans la direction x, g d´ecroissant en s’eloignant du bord. Exemple: 